13. 一次遅れ要素(1次遅れ系)の時間応答
制御要素に入力信号を加えて出力信号を得たとき、出力信号の位相が入力信号の位相よりも遅れる場合、これを遅れ要素という。一次遅れ要素は、伝達関数の分母がsの一次式となる場合をいう。なお、位相の変化は、0°~-90°の範囲である。
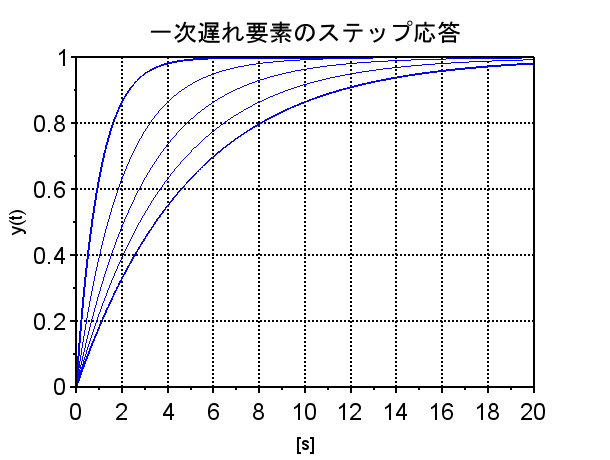
ステップ応答、\(y(t)=1-e^{-\frac{1}{T}t} \)より、
\(t\rightarrow\infty\) \(y(t)\rightarrow1\)
\(\frac{dy(0)}{dt}=\frac{1}{T}\)なので、\(y(0)\)における接線の式は、\(z(t)=\frac{1}{T}t\)となる。従って、\(t=T\)において \(z(T)=1\) (\(y(t)\)の最終値)となる。
この\(T\)を時定数という。
*一次遅れ要素(1次遅れ系)
$$G(s)=\frac{K}{Ts+1}=\frac{K}{T}\cdot\frac{1}{s+\frac{1}{T}} (T>0,K>0) $$
\(K=1\)としたときの標準形は、
$$G(s)=\frac{1}{Ts+1}=\frac{1}{T}\cdot\frac{1}{s+\frac{1}{T}} $$
・単位インパルス応答
$$g(t)=\mathcal {L^{-1}}\{G(s)\}=\frac{1}{T}e^{-\frac{1}{T}t}$$
・単位ステップ応答
単位ステップ信号:\(U(s)=\mathcal{L}\{I(t)\}=\frac{1}{s}\)より、
$$Y(s)=G(s)U(s)=\frac{1}{Ts+1}\cdot\frac{1}{s}=\frac{1}{s}-\frac{1}{s+\frac{1}{T}}$$
\(y(t)=\mathcal{L}^{-1}\{Y(s)\}=\mathcal{L^{-1}}\left\{\frac{1}{s}-\frac{1}{s+\frac{1}{T}}\right\} \\=1-e^{-\frac{1}{T}t}\)
1次遅れ要素のステップ応答の図から時定数Tが大きくなると応答の立ち上がりが緩やかになり、時間遅れが生じていることが分かる。ここで入力信号が正弦波と仮定すると、時定数が大きいほど位相遅れが大きくなる(入力信号に対して出力信号が遅れる)と考えることができる。
Scilabによる一次遅れ要素の解析(ステップ応答)
//1次遅れ系のステップ応答
clear; clf();
s=%s;
//時定数 T (時定数を1.0から1.0刻みで5.0まで変える)
for T=1.0:1.0:5.0
G=1/(T*s+1); /* 一次遅れ要素の伝達関数 */
Gs=syslin('c',G); /* Scilab内部のシステム表現に変換 */
//ステップ応答
t=0:0.01:20; /* 0から20まで0.01刻みでtを設定 */
y=csim('step',t,Gs); /* 線形シミュレーション関数 */
scf(0); /* プロット画面の設定 */
plot(t,y);xgrid; /* プロット関数、グリッドを付ける */
end; /* for 繰り返し区間 */
Scilabで一次遅れ要素のステップ応答を求める基本的なスクリプトを示す。
一次遅れ要素のステップ応答の図は、これで描いたもので、プロット図の軸の修飾などは、プロット図の編集項目で行った。この修飾(軸に名前を付けたりフォントを大きくすることなど)はスクリプト中に記述できるが、スクリプトが煩雑になり本質部分が分かりにくくなるので、最終的に必要なプロット図だけを選んで編集した方が良いと思う。
Scilab help ← 各関数の詳細はこちらで確認願います。


“13. 一次遅れ要素(1次遅れ系)の時間応答” に対して4件のコメントがあります。
コメントは受け付けていません。