15. むだ時間要素の時間応答

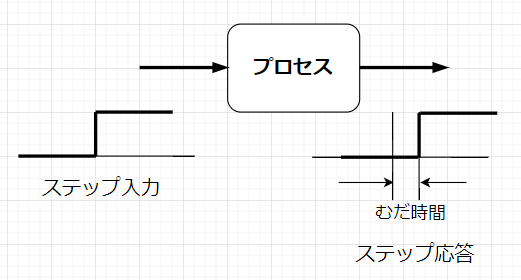
むだ時間要素は時間遅れ要素の一種だが、１,２次遅れ要素とは違った特性を持っている。 図で示すような機能でベルトコンベアや配管による液体輸送などが実施のプロセスとなる。例えばベルトコンベアの始端に荷物を載せた場合、終端に届くまでの時間がむだ時間となる。コンベア速度が一定であればむだ時間は一定となる。時間領域での式は、入力を\(u(t)\)、出力を\(y(t)\)とすると、むだ時間は次の式で表される。$$y(t)=u(t-L)$$\(L\)がむだ時間である。

\(y(t)=u(t-L)\)をラプラス変換すると、$$Y(s)=\int_{0}^{\infty}u(t-L)e^{-st}dt$$ となる。　\(0\le t \lt L\)のとき\(u(t-L)=0\)なので、\(\tau=t-L\)と変数変換して\(\tau\)で積分すると、　$$Y(s)=\int_{L}^{\infty}u(t-L)e^{-st}dt$$ $$=\int_{0}^{\infty}u(\tau)e^{-s(\tau+L)}d\tau$$ $$=U(s)e^{-Ls}$$ となる。従って、むだ時間要素の伝達関数は、$$G(s)=\frac{Y(s)}{U(s)}=e^{-Ls}$$ となる。これは有理関数ではないので、\(s=0\)の周りでマクローリン展開してべき級数で扱うことが多い。$$G(s)=1+\frac{(-Ls)}{1!}+\frac{(-Ls)^2}{2!}+\cdots$$ $$+\frac{(-Ls)^k}{k!}+\cdots$$ 時間応答は図のようにむだ時間（\(L\)）遅れるだけで入力と同様になる。