15. 状態観測器に基づいた制御系

状態観測器に基づいた制御系は、制御対象の状態量を観測することで、操作量を生成する制御システムである。この制御系では、状態フィードバック制御を基本として、制御対象の状態変数をフィードバックすることで、制御対象の安定化と望ましい応答を実現することを目指す。
状態観測器は、制御対象の入力と出力を観測して、制御対象内部の状態変数を推定する。これにより、操作量を生成するための情報を得ることができる。状態観測器は、制御対象の状態方程式と出力方程式を使用して設計する。
状態フィードバック制御では、状態観測器によって推定された状態変数を使用して、操作量を決定する。操作量は、制御対象への入力で、制御対象の出力は、状態観測器によって観測され、フィードバックされることになる。
状態フィードバック制御は、制御対象の内部状態を制御することができるため、外乱やノイズの影響に強く、高速で正確な制御が可能である。ただし、状態観測器には計算コストがかかるため、高速なシステムでは実現が難しい場合がある。

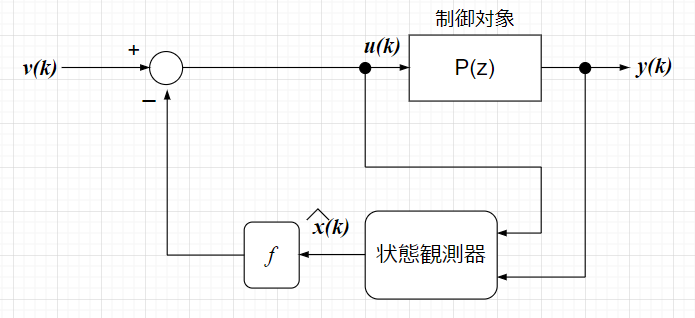
状態フィードバックの操作量 \(u(k)=-f x(k)+v(k)\)において、状態変数\(x(k)\)が観測できない場合、その状態の推定値 \(\hat{x} (k)\)でフィードバックをかけるとする。すなわち、操作量を\(u(k)=-f \hat{x} (k)+v(k)\)　とする。
このとき、閉ループ系は、$$\begin{bmatrix} x( k+1) \\ \hat{x}(k+1) \end{bmatrix} = \begin{bmatrix} A & -b f \\ gc & A - bf -gc \end{bmatrix} \begin{bmatrix} x(k) \\ \hat{x}(k) \end{bmatrix} + \begin{bmatrix} b \\ b \end{bmatrix} v(k) \\ y(k) = \begin{bmatrix} c & 0 \end{bmatrix} \begin{bmatrix} x(k) \\ \hat{x}(k) \end{bmatrix} $$となる。
ここで、$$\begin{bmatrix} x(k) \\ e(k) \end{bmatrix} = \begin{bmatrix} I & 0 \\ I & -I \end{bmatrix} \begin{bmatrix} x(k) \\ \hat{x}(k) \end{bmatrix}$$とおくと、$$\begin{bmatrix} x(k+1) \\ e(k+1) \end{bmatrix} = \begin{bmatrix} A - bf & bf \\ 0 & A - gc \end{bmatrix} \begin{bmatrix} x(k) \\ e(k) \end{bmatrix} + \begin{bmatrix} b \\ 0 \end{bmatrix} v(k) \\ y(k) = \begin{bmatrix} c & 0 \end{bmatrix} \begin{bmatrix} x(k) \\ e(k) \end{bmatrix}$$となる。
特性方程式は、$$\left|zI -\begin{bmatrix} A - bf & bf \\ 0 & A - gc \end{bmatrix}\right| = 0$$なので、 $$|zI - (A - bf)|\cdot |zI -(A -gc)| = 0$$となる。これより、\((A-bf)\)の固有値と\((A-gc)\)の固有値を個別に配置できることがわかる。

状態観測器を使った状態フィードバックシステムの伝達関数

$$\begin{bmatrix} x(k+1) \\ e(k+1) \end{bmatrix} = \begin{bmatrix} A - bf & bf \\ 0 & A - gc \end{bmatrix} \begin{bmatrix} x(k) \\ e(k) \end{bmatrix} + \begin{bmatrix} b \\ 0 \end{bmatrix} v(k) \\ y(k) = \begin{bmatrix} c & 0 \end{bmatrix} \begin{bmatrix} x(k) \\ e(k) \end{bmatrix}$$において、Z変換すると、$$zI \begin{bmatrix} x(z) \\ e(z) \end{bmatrix} = \begin{bmatrix} A - bf & bf \\ 0 & A - gc \end{bmatrix} \begin{bmatrix} x(z) \\ e(z) \end{bmatrix} + \begin{bmatrix} b \\ 0 \end{bmatrix} v(z) \\ y(z) = \begin{bmatrix} c & 0 \end{bmatrix} \begin{bmatrix} x(z) \\ e(z) \end{bmatrix}$$ となる。よって、$$\begin{bmatrix} x(z) \\ e(z) \end{bmatrix} =\left\{ zI - \begin{bmatrix} A - bf & bf \\ 0 & A - gc \end{bmatrix} \right\}^{-1} \begin{bmatrix} b \\ 0 \end{bmatrix} v(z)$$ さらに、$$y(z) = \begin{bmatrix} c & 0\end{bmatrix} \begin{bmatrix} zI - (A-bf) & -bf \\ 0 & zI - (A-gc) \end{bmatrix} ^{-1} \begin{bmatrix} b \\ 0 \end{bmatrix} v(z) \\ = c\left[ zI - (A- bf) \right]^{-1} b v(z)$$　よって、$$G(z) = \frac{y(z)}{v(z)} = c\left[ zI - (A- bf) \right]^{-1} b$$となる。
すなわち、伝達関数は状態観測器に依存しないことがわかる。