8. 最小二乗法
最小二乗法は、統計学や数学において、データの間に線形関係がある場合にその関係を表現するために使用される手法の1つで、計測工学では最小二乗法は、実測データとモデル予測値との間の誤差を最小化することで、最も適切なモデルを見つけるために使用されることが多い。
最小二乗法(一次関数で近似する場合)では、データポイントの座標を使用して、最もよくフィットする直線を見つけることが目的でとなる。この直線は、実際のデータと直線との距離の平方の和が最小となるように決定される。つまり、最小二乗法では、予測される値と実際の値との誤差を最小化するように直線を選択することになる。
計測工学での一般的な最小二乗法は、以下の手順で実行される。
1.実測データを収集する。
2.モデルの式を選択する。モデルは入力変数と出力変数の間の関係を表す。
3.モデルのパラメータを推定する。最小二乗法では、モデルのパラメータを実測データとモデルの予測値との誤差を最小化するように推定する。
4.推定されたパラメータを使用して、モデルの予測値を計算する。
5.モデルの予測値と実測データを比較し、誤差を計算する。
6.誤差が許容範囲内になるまで、モデルのパラメータを調整する。
最小二乗法は、測定データに対してモデルを適合させるためにも使用される。これは、例えば、測定データから得られた複数の値の平均値を求める場合や、測定データから得られた関数の近似値を求める場合などに使用される。
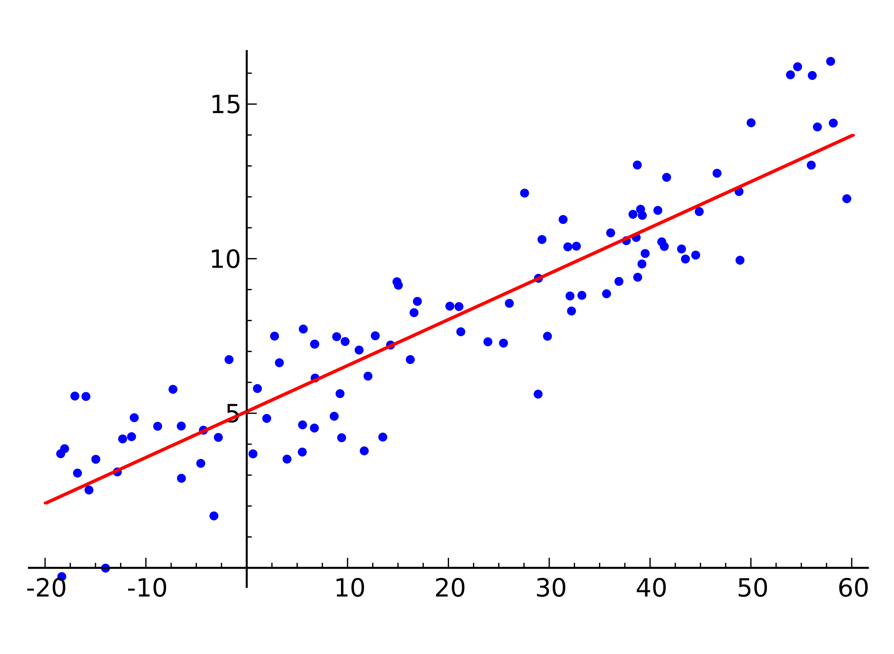
最小二乗法
測定で得られた数値の組を、適当なモデルとして想定される1次関数などの関数を用いて近似するとき、その関数が測定値に対してよい近似となるように、モデルとした関数の値と測定値との差の二乗の和が最小となるようにモデルとした関数の係数を決定する方法。
図「最小二乗法の例」では、測定値(青点)を1次関数(赤線)で近似している。すなわち、1次関数の傾きと切片を測定値から決定している。
最小二乗法の原理
*前提条件
最小二乗法では測定データ\( y\) はモデル関数 \(f(x)\) と誤差\(\epsilon\)の和で \(y = f(x) + \epsilon\)と表せるとする。
測定データが偶然誤差を含んでいるとき、正規分布になると期待される。
※最小二乗法の理論的な前提
・測定値の誤差には偏りがない。すなわち誤差の平均値は 0 である。
・測定値の誤差の分散は既知である。
・各測定は互いに独立であり、誤差の共分散は 0 である。
・誤差は正規分布する。
・\(m\) 個のパラメータを含むモデル関数\(f\) が知られていて、測定量の真の値を近似誤差なく再現することのできるパラメータが存在する。
共分散とは
共分散( covariance)は、統計学や確率論において、2つの確率変数の間の関係を表す指標の1つである。2つの変数の同時変動の度合いを表す数値。共分散の値が0である場合には、2つの変数の間には相関関係がないことを示している。
最小二乗法の基礎(一次関数で近似する場合)
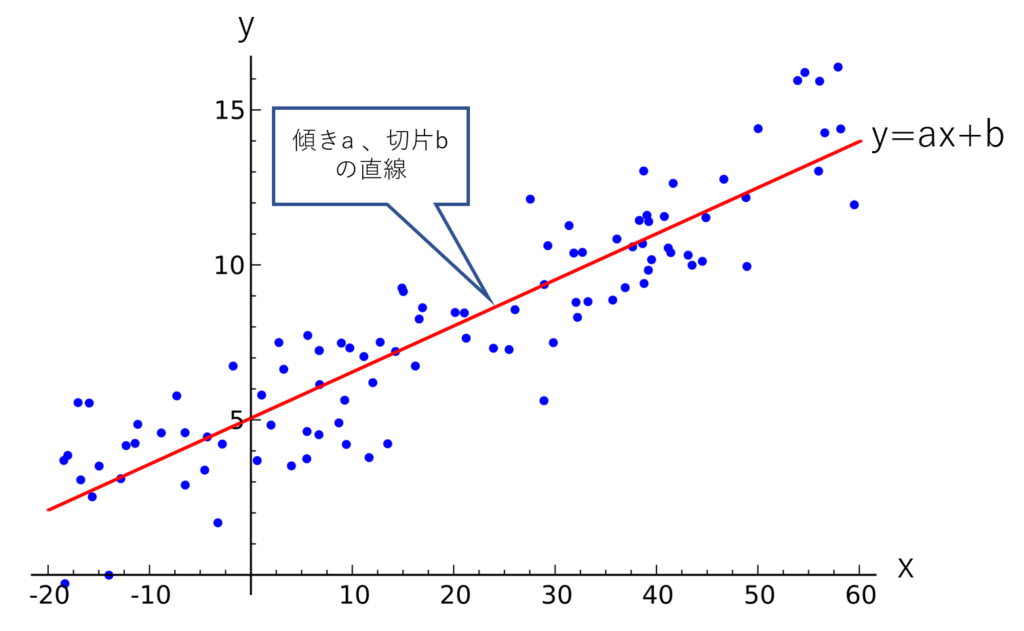
測定データ\((x_1,y_1 )\;,\; (x_2,y_2 )\;,\; (x_3,y_3 )\;,\cdots,\; (x_n,y_n )\) の\(n\)個のデータがあるとして、次の図に示すように、一次関数(直線)で近似できるとする。
一次関数:\(y=ax+b\) \(a\):傾き \(b\):切片 を決定する。
\(x\) の \(i\)番目のときのデータ\(y\) は、\(y_i\) なので\( (x_i,y_i )\) であり、一次関数からは、\((x_i, ax_i+b)\) となる。
\( y_i\) と\(ax_i+b\) の差(距離)が全てのデータにおいて、小さくなるようにするには、各点の距離の総和が最小になる\( a,b\) を見つければよい。
各点の距離の総和\(\epsilon(a,b)\)は、$$\epsilon(a,b) = \sum_{i=1}^n \left\{y_i-(ax_i+b)\right\}^2$$ と表せる。この式を展開整理すると、$$\epsilon(a,b) = \sum_{i=1}^n \left(x_i^2 a^2 - 2x_i y_i a + 2x_i ab + b^2 - 2y_i b+y_i^2 \right) $$となり、求めたい\((a,b)\)の2変数関数となっている。この式の最小値を求めたい。
\(b\)を固定して考えると、\(a\)の2次関数となり、\(a\)の2乗の係数が正なので下に凸の関数と考えることができる。従って、\(a\)で微分(偏微分)した関数の0の点が極小値(最小値の候補)となる。
\(a\)を固定して考えると、\(b\)の2次関数となり、\(b\)の2乗の係数が正なので下に凸の関数と考えることができる。従って、\(b\)で微分(偏微分)した関数の0の点が極小値(最小値の候補)となる。
・\(\epsilon(a,b)\)の\(a\)による偏微分は、$$\frac{\partial \epsilon(a,b)}{\partial a} =\sum_{i=1}^n (2x_i^2 a + 2x_i b - 2x_i y_i ) = -2\sum_{i=1}^n x_i (y_i - ax_i - b)$$・\(\epsilon (a,b)\)の\(b\)による偏微分は、$$\frac{\partial \epsilon(a,b)}{\partial b} = \sum_{i=1}^n (2x_i a + 2b - 2y_i ) = -2\sum_{i=1}^n (y_i - ax_i - b)$$上式=0が極小値を示す点となる。$$\frac{\partial \epsilon(a,b)}{\partial a}=0 \;\;\; , \;\;\; \frac{\partial \epsilon(a,b)}{\partial b} = 0$$より、$$a \sum_{i=1}^n x_i ^2 + b \sum_{i=1}^n x_i = \sum_{i=1}^n x_i y_i \cdots \cdots (1)$$ $$a \sum_{i=1}^n x_i + b n =\sum_{i=1}^n y_i \cdots \cdots (2)$$ \((x_1,y_1 )\;,\; (x_2,y_2 )\;,\; (x_3,y_3 )\;,\cdots,\; (x_n,y_n )\)の\(n\)個の測定データで、\((1),(2)\)式は各\(n\)個の1次式で変数が2個\((a,b)\)なので、\(n\)個の連立方程式となり、これを解けば\(a,b\)が求まる。これらの式をさらに整理する。\((2)\)式の両辺を\(n\)で割ると、$$a \bar{x} + b = \bar{y} \;\;\;\;\; \bar{x} = \frac{\sum_{i=1}^n x_i}{n} \;\;\;\;\; \bar{y} = \frac{\sum_{i=1}^n y_i}{n}$$ \(\bar{x}\)は測定値\(x_i\)の平均値、 \(\bar{y}\)は測定値\(y_i\)の平均値となる。\(b = -a \bar{x} + \bar{y}\)を\((1)\)式に代入すると、$$a \sum_{i=1}^{n} x_i^2 + (-a \bar{x} + \bar{y})\sum_{i=1}^n x_i = \sum_{i=1}^n x_i y_i$$となる。この両辺を\(n\)で割り、\(a\)について解くと、$$a\left( \frac{\sum_{i=1}^n x_i ^2}{n} - \bar{x} \frac{\sum_{i=1}^n xi}{n} \right) = \frac{\sum_{i=1}^n x_i y_i}{n} - \bar{y} \frac{\sum_{i=1}^n x_i}{n} $$ここで、$$\bar{x} = \frac{\sum_{i=1}^n x_i}{n} \;\;\; \overline{x^2} = \frac{\sum_{i=1}^n x_i ^2}{n} \;\;\; \overline{xy} = \frac{\sum_{i=1}^n x_i y_i}{n} \;\;\; \bar{y}=\frac{\sum_{i=1}^n y_i}{n}$$なので、$$a = \frac{\overline{xy} - \bar{x}\cdot\bar{y}}{\overline{x^2} - \bar{x}^2} = \frac{\sigma_{xy}}{\sigma_x^2} \;\;\;,\;\;\; b = -a\bar{x} + \bar{y}$$となる。
\(\sigma_x^2\)は\(x\)の分散、\(\sigma_{xy}\)は\(x,y\)の共分散である。
従って、傾き\(a\)は、\(x,y\)の共分散と\(x\)の分散、切片\(b\)は、\(a\)と\(x\)の平均値、\(y\)の平均値から求まることになる。以上により、測定データから直線の式の \(a\):傾き 、\(b\):切片 が決定できる。
参考
【分散公式】 $$\sigma_x^2 = \frac{1}{n} \sum_{i=1}^n (x_i -\bar{x})^2 =\frac{1}{n} \sum_{i=1}^n (x_i^2 - 2x_i \bar{x} + \bar{x}^2) \\ = \frac{1}{n} \sum_{i=1}^n x_i^2 - 2\bar{x} \frac{1}{n} \sum_{i=1}^n x_i + \frac{1}{n} \cdot n \bar{x}^2 \\ = \frac{1}{n} \sum_{i=1}^n x_i^2 - 2\bar{x}^2 + \bar{x}^2 \\ = \frac{1}{n} \sum_{i=1}^n x_i^2 - \bar{x}^2 = \overline{x^2} - \bar{x}^2$$
$$\sigma_{xy} = \frac{1}{n} \sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y}) \\ = \frac{1}{n} \sum_{i=1}^n x_i y_i - \frac{1}{n} \sum_{i=1}^n x_i \bar{y} - \frac{1}{n} \sum_{i=1}^n \bar{x} y_i + \frac{1}{n} \sum_{i=1}^n \bar{x} \cdot \bar{y} \\ = \overline{xy} - \bar{y} \frac{1}{n} \sum_{i=1}^n x_i - \bar{x} \frac{1}{n} \sum_{i=1}^n y_i + \frac{1}{n} \cdot n\bar{x} \cdot \bar{y} = \overline{xy} - \bar{x} \cdot \bar{y}$$
【2変数関数の偏微分の定義】
偏微分とは、多変数関数を「特定の文字以外定数だとみなして」微分したもののことである。
・1変数関数\(f(x)\)の微分:変数を少し動かしたときの変化の割合 $$ \frac{df(x)}{dx} = \lim_{h \rightarrow 0} \frac{f(x+h) -f(x)}{h}$$
・2変数関数\(f(x,y)\)の偏微分:特定の一つの変数のみを少し動かしたときの関数 \(f(x,y)\) の変化の割合
関数\(f(x,y)\)の\(x\)についての偏微分(\(y\)は固定)$$\frac{\partial f(x,y)}{\partial x} = \lim_{h \rightarrow 0} \frac{f(x+h, y) -f(x,y)}{h}$$
関数\(f(x,y)\)の\(y\)についての偏微分(\(x\)は固定)$$\frac{\partial f(x,y)}{\partial y} = \lim_{h \rightarrow 0} \frac{f(x, y+h) -f(x,y)}{h}$$


“8. 最小二乗法” に対して2件のコメントがあります。
コメントは受け付けていません。