22. フィードバックの構成
制御対象の基本構造
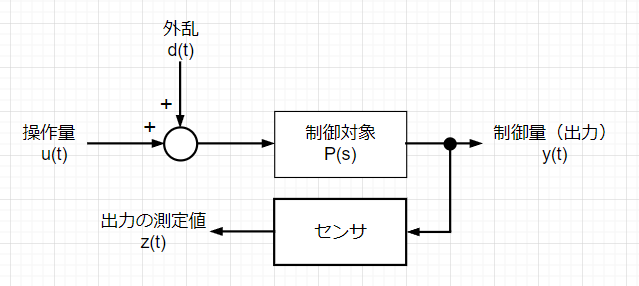
制御対象の基本構造は、図のように表せる。制御対象\(P(s)\)には何らかの駆動機構(アクチュエータ)があり、それに操作量\(u(t)\)を加えることで制御対象\(P(s)\)の状態を変化させることができる。この操作量には一般的に雑音や外力などの外乱\(d(t)\)が加わる。制御対象\(P(s)\)からは制御量が得られる。
例えば、制御対象がモータであれば、軸の回転角度や角速度などが制御量となる。この制御量の一部が出力\(y(t)\)として使われる。この出力はセンサにより出力の測定値\(z(t)\)として検出され、操作量\(u(t)\)の決定や制御対象の状態把握などに利用される。
フィードフォワード制御系
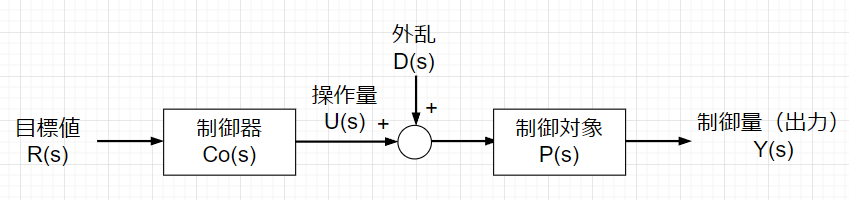
フィードフォワード制御系は、図より次のような式で表せる。$$Y(s)=P(s)\left\{U(s)+D(s)\right\},$$ $$U(s)=C_o(s)R(s)$$よって、$$Y(s)=C_o(s)P(s)R(s) + P(s)D(s)$$となる。
フィードフォワード制御系では、外乱\(D(s)=0\)ならば、制御器を\(C_o(s)=\frac{1}{P(s)}\)とすることで、$$Y(s)=C_o(s)P(s)R(s)=\frac{1}{P(s)} P(s)R(s)=R(s)$$となり、出力\(Y(s)\)を目標値\(R(s)\)に一致させることができる。 しかし、外乱\(D(s)\)の影響は、出力に\(Y(s)=P(s)D(s)\)と現れる。すなわち、外乱\(D(s)\)の影響は制御器\(C_o(s)\)では抑制できないことになる。
フィードバック制御系
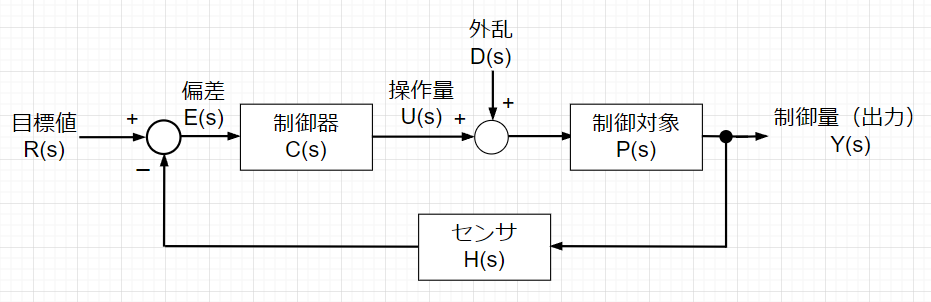
フィードバック制御系は、図より次のように表せる。
$$Y(s)=P(s)\left\{U(s)+D(s)\right\},$$ $$U(s)=C(s)E(s), E(s)=R(s)-H(s)Y(s)$$
よって、$$Y(s)=P(s)\left[C(s)\left\{R(s)-H(s)Y(s)\right\}+D(s)\right]$$ $$Y(s)\left(1+P(s)C(s)H(s)\right)$$ $$=P(s)C(s)R(s)+P(s)D(s)$$$$Y(s)=\frac{P(s)C(s)}{1+P(s)C(s)H(s)}\cdot R(s) +$$ $$ \frac{P(s)}{1+P(s)C(s)H(s)}\cdot D(s)$$となる。
これより、目標値\(R(s)\)から出力\(Y(s)\)までと、外乱\(D(s)\)から出力\(Y(s)\)までの特性は、制御器\(C(s)\)によって調整できることが分かる。
単位フィードバック制御系
前記のフィードバック制御系で、\(H(s)=1\)とした場合を単位フィードバック制御系(直結フィードバック制御系)という。
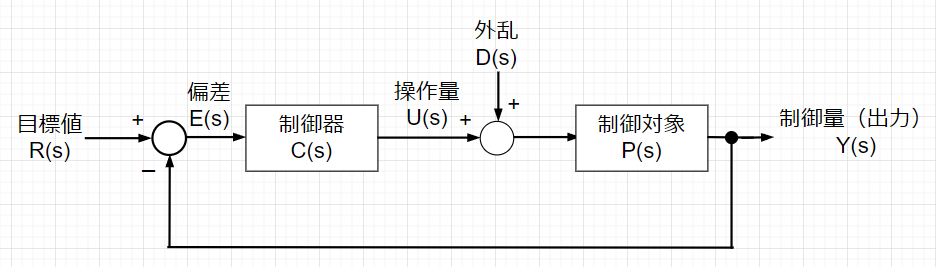
単位フィードバック制御系は、ブロック線図から以下の式で表せる。$$E(s)=R(s)-Y(s), $$ $$U(s)=C(s)E(s), Y(s)=P(s)\left\{U(s)+D(s)\right\}$$従って、$$Y(s)=P(s)\left[C(s)\left\{R(s)-Y(s)\right\}+D(s)\right]$$ $$Y(s)\left(1+P(s)C(s)\right)$$ $$=P(s)C(s)R(s)+P(s)D(s)$$よって、$$Y(s)=\frac{P(s)C(s)}{1+P(s)C(s)}\cdot R(s)$$ $$+\frac{P(s)}{1+P(s)C(s)}\cdot D(s)$$
ここで、\(L(s)=P(s)C(s)\)を開ループ伝達関数(一巡伝達関数)と呼ぶ。\(D(s)=0\)とすると、\(Y(s)=\frac{P(s)C(s)}{1+P(s)C(s)}\cdot R(s)\)なので、$$T(s)=\frac{Y(s)}{R(s)}=\frac{P(s)C(s)}{1+P(s)C(s)}$$となり、これを閉ループ伝達関数(相補感度関数)と呼ぶ。また、\(R(s)=0\)とすると、\(Y(s)=\frac{P(s)}{1+P(s)C(s)}\cdot D(s)\)なので、$$\frac{Y(s)}{D(s)}=\frac{P(s)}{1+P(s)C(s)}$$となり、外乱抑圧特性となる。
\(D(s)=0\)として、\(R(s)-E(s)\)間の伝達関数を求めると、$$S(s)=\frac{E(s)}{R(s)}=\frac{1}{1+P(s)C(s)}$$となり、感度関数と呼ぶ。\(L(s)=P(s)C(s)\)を使って表すと、
閉ループ伝達関数(相補感度関数):$$T(s)=\frac{L(s)}{1+L(s)}$$感度関数:$$S(s)=\frac{1}{1+L(s)}$$外乱抑圧特性:$$\frac{Y(s)}{D(s)}=\frac{P(s)}{1+L(s)}$$なお、$$T(s)+S(s)=1$$なので、感度関数と相補感度関数はトレードオフの関係となる。
また上式より、これらの伝達関数の特性方程式は、$$1+L(s)=0$$である。
フィードフォワード制御系の問題点
制御対象\(P(s)=\frac{1}{2s-1}\)があったとする。このシステムの極は\(p=\frac{1}{2}\)で、複素平面の右半平面のあるため、\(P(s)\)は不安定である。また、インパルス応答は、\(\mathcal{L}^{-1}\left\{P(s)\right\}=\frac{1}{2}e^{\frac{1}{2}t}\)なので、\(t \rightarrow \infty\)で、\(g(t) \rightarrow \infty\)となり発散する。つまり、不安定なシステムである。
ここで、フィードフォワード制御器を\(C_o(s)=\frac{3(2s-1)}{2s^2+s+2}\)とすると、制御システムは$$P(s)C_o(s)=\frac{1}{2s-1} \cdot \frac{3(2s-1)}{2s^2+s+2} $$ $$= \frac{3}{2s^2+s+2}$$となり、制御システムの極は\(p=\frac{-1 \pm j\sqrt{15}}{4}\)となり、安定なシステムとなる。これは、制御対象\(P(s)\)の不安定な極を制御器\(C_o(s)\)の零点で相殺したことで実現できている(極零相殺)。
しかし、この方法では制御器の零点や制御対象の極が少しでも変化すると、不安定極が顕在化し制御システムは不安定となってしまう。
一方、フィードバック制御系では、制御器\(C(s)=\frac{3}{s+1}\)とすると、\(L(s)=P(s)C(s)=\frac{1}{2s-1} \cdot \frac{3}{s+1}\)なので、閉ループ制御系の伝達関数\(T(s)\)は、$$T(s)=\frac{L(s)}{1+L(s)}=\frac{\frac{1}{2s-1}\cdot \frac{3}{s+1}} {1+\frac{1}{2s-1}\cdot \frac{3}{s+1}}$$ $$=\frac{3}{2s^2+s+2}$$となる。制御システムの伝達関数はフィードフォワード制御系とフィードバック制御系で同じになるため、応答特性は同じにできるが、フィードバック制御系では極零相殺をしていないので、制御器や制御対象の極が少し変化しても不安定になることはない。

