13. Δ-Y変換、Y-Δ変換

Δ-Y変換（デルタ‐スター変換）とY-Δ変換（スター‐デルタ変換）は、電気回路の解析や設計において、Δ型回路（三角形回路）とY型回路（星型回路）の相互変換に使用される。
Δ型回路では、3つの抵抗器が3つの交差点で接続されている。この回路をY型回路に変換するには、3つの抵抗器が１つの共通接点で接続されるように変換する。
また、Y型回路では、3つの抵抗器が1つの交差点で接続されている。この回路をΔ型回路に変換するには、3つの抵抗器が3つの交差点で接続されるように変換する。
これらの変換は、複雑な回路を単純な形に変換するために使用され、回路の特性を理解するために重要である。

Δ-Y変換

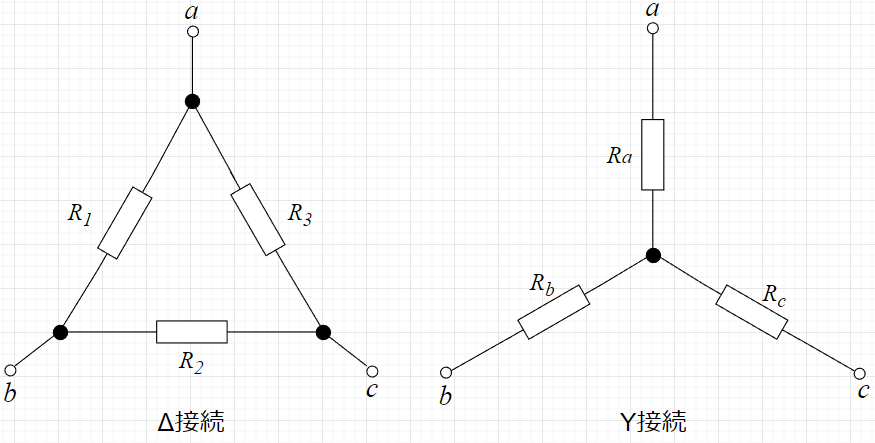
Δ接続とY接続が等価となる抵抗値（\(R_1,R_2,R_3,R_a,R_b,R_c\)）を考える。つまり、端子間（\(a-b\;,\;b-c\;,\;c-a\)）の抵抗値が等しくなるように各抵抗の値を決定する。

Δ接続の端子\(a-b\)間の抵抗値\(R_{ab}\)は、\(R_1\)と（\(R_2 + R_3\)）の並列抵抗値となる。（端子\(c\)は何も接続されていないと考えれば良い。）$$R_{ab} = \frac{R_1(R_2 + R_3)}{R_1+ R_2 + R_3}=\frac{R_1 R_2 + R_1 R_3}{R_1+ R_2 + R_3}$$同様に、端子\(b-c\)間の抵抗値\(R_{bc}\)、端子\(c-a\)間の抵抗値\(R_{ca}\)は、それぞれ、$$R_{bc} = \frac{R_2(R_3 + R_1)}{R_1 + R_2 + R_3}= \frac{R_2 R_3 +R_2 R_1}{R_1 + R_2 + R_3}\\ R_{ca} = \frac{R_3(R_1 + R_2)}{R_1 + R_2 + R_3} = \frac{R_3 R_1 +R_3 R_2}{R_1 + R_2 + R_3}$$となる。
一方、Y接続の端子\(a-b\)間の抵抗値\(R_{ab}\)は、\(R_a\)と\(R_b\)の直列接続となる。$$R_{ab} = R_a + R_b$$同様に、端子\(b-c\)間の抵抗値\(R_{bc}\)、端子\(c-a\)間の抵抗値\(R_{ca}\)は、それぞれ、$$R_{bc} = R_b + R_c \\ R_{ca} = R_c + R_a$$となる。
Δ接続、Y接続の端子間の各抵抗値が等しいとき、Δ-Y変換できるので、$$\frac{R_1 R_2 + R_1 R_3}{R_1+ R_2 + R_3} = R_a + R_b \\ \frac{R_2 R_3 + R_2 R_1}{R_1 + R_2 + R_3} = R_b + R_c \\ \frac{R_3 R_1 +R_3 R_2}{R_1 + R_2 + R_3} = R_c + R_a$$が成立する必要がある。各式を整理して比較する。$$\frac{R_1 R_2}{R_1+ R_2 + R_3} + \frac{R_1 R_3}{R_1+ R_2 + R_3} = R_a + R_b \\ \frac{R_2 R_3}{R_1+ R_2 + R_3} + \frac{R_2 R_1}{R_1+ R_2 + R_3} = R_b + R_c \\ \frac{R_3 R_1}{R_1+ R_2 + R_3} + \frac{R_3 R_2}{R_1+ R_2 + R_3} = R_c + R_a$$これより、$$R_a = \frac{R_3 R_1}{R_1+ R_2 + R_3} \\ R_b = \frac{R_1 R_2}{R_1+ R_2 + R_3} \\ R_c = \frac{R_2 R_3}{R_1+ R_2 + R_3} $$となる。
以上より、Δ接続の\(R_1,R_2,R_3\)と等価なY接続の\(R_a,R_b,R_c\)が求まる。

なお、Δ接続での抵抗値が全て等しい場合、つまり、\(R_1 = R_2 =R_3 =R\)　のとき、Y接続での抵抗値は、$$R_a = R_b = R_c = \frac{R}{3}$$となる。

Y-Δ変換

先に求めた、$$R_a = \frac{R_3 R_1}{R_1+ R_2 + R_3} \;\; \cdots \cdots (1) \\ R_b = \frac{R_1 R_2}{R_1+ R_2 + R_3} \;\; \cdots \cdots (2) \\ R_c = \frac{R_2 R_3}{R_1+ R_2 + R_3} \;\; \cdots \cdots (3)$$の関係より、$$R_a R_b = \frac{R_1^2 R_2 R_3}{(R_1 + R_2 +R_3)^2} \\ R_b R_c = \frac{R_2^2 R_1 R_3}{(R_1 + R_2 +R_3)^2} \\ R_c R_a = \frac{R_3^2 R_1 R_2}{(R_1 + R_2 +R_3)^2}$$ さらに、これらを加算すると、$$R_a R_b + R_b R_c + R_c R_a =\frac{R_1 R_2 R_3 (R_1 + R_2 +R_3)}{(R_1 + R_2 + R_3)^2} = \frac{R_1 R_2 R_3}{R_1 + R_2 + R_3} $$ ここで、式(3)を使うと、$$R_a R_b + R_b R_c + R_c R_a = R_1 R_c$$ よって、$$R_1 = \frac{R_a R_b + R_b R_c + R_c R_a}{R_c}$$となる、同様に、式(2)を使うと、$$R_a R_b + R_b R_c + R_c R_a = R_3 R_b$$より、$$R_3 = \frac{R_a R_b + R_b R_c + R_c R_a}{R_b}$$また、式(1)を使うと、$$R_a R_b + R_b R_c + R_c R_a = R_2 R_a$$より、$$R_2 = \frac{R_a R_b + R_b R_c + R_c R_a}{R_a}$$が求まる。まとめると、$$R_1 = \frac{R_a R_b + R_b R_c + R_c R_a}{R_c} \\R_2 = \frac{R_a R_b + R_b R_c + R_c R_a}{R_a} \\R_3 = \frac{R_a R_b + R_b R_c + R_c R_a}{R_b}$$である。
以上より、Y接続の\(R_a,R_b,R_c\)と等価なΔ接続の\(R_1,R_2,R_3\)が求まる。

なお、Y接続での抵抗値が全て等しい場合、つまり、\(R_a = R_b =R_c =R\)　のとき、Δ接続での抵抗値は、$$R_1 = R_2 = R_3 = 3R$$となる。