19. 交流電流、交流電圧

交流電力（交流電圧、交流電流）は、主に旋回磁場による発生法、すなわち発電機によって得られる。これは、回転子に取り付けられた永久磁石と、固定子に巻かれたコイルによって、磁界と電界を相互に作用させることにより、交流電力を発生する方法で、水力発電、風力発電、火力発電、原子力発電などで広く使用されている。
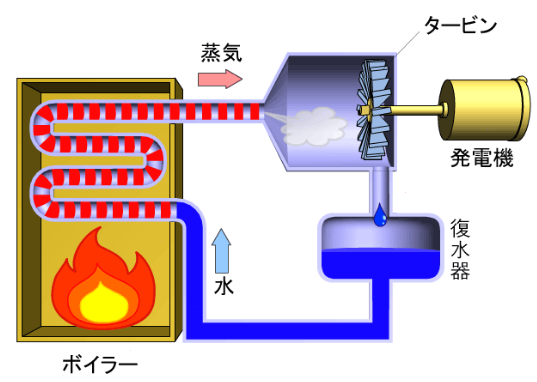
図「火力発電のしくみ」にあるように、発電機は回転機器（同期発電機）であるため、発電される電力は、交流となる。
・三相同期発電機の原理と構造は、こちらを参考に。

周期的に繰り返す自然な変化は、三角関数の正弦および余弦で表される形をしている。このような波は、数学的に取り扱いやすく、さらに任意の周期的な波形は、多くの正弦波の和によって表すことができる。
正弦波は最も基本的波形であるので、交流はほとんど正弦波として取り扱っている。
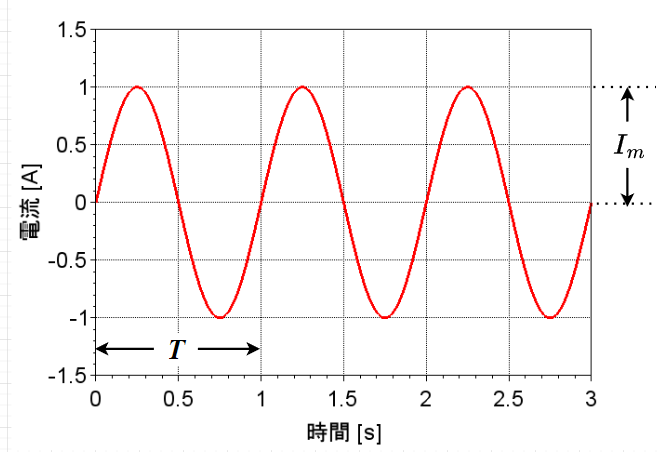
図「交流電流波形」で、振幅\(I_m\) [A]、周期\(T\) [s]とすると、正弦波電流波形は、$$i(t) = I_m \sin \omega t \; [A]$$と表せる。この\(i(t)\)を瞬時値という。ここで、\(\omega = 2 \pi f\) [rad/s]、\(f =1/T\) [Hz]である。\(\omega\) ：角周波数、\(f\)：周波数である。周波数\(f\)は、1秒間に周期が何回あるかを意味しており、\(1 \div T\)なので、周期\(T\)の逆数になる。また、正弦関数で表しており、一周期で\(2\pi\)[rad]となり、\(t=T\)のとき\(\omega T = 2\pi \)となるので、\(\omega = 2 \pi /T =2 \pi f \; [\mathrm{rad} /s]\)である。

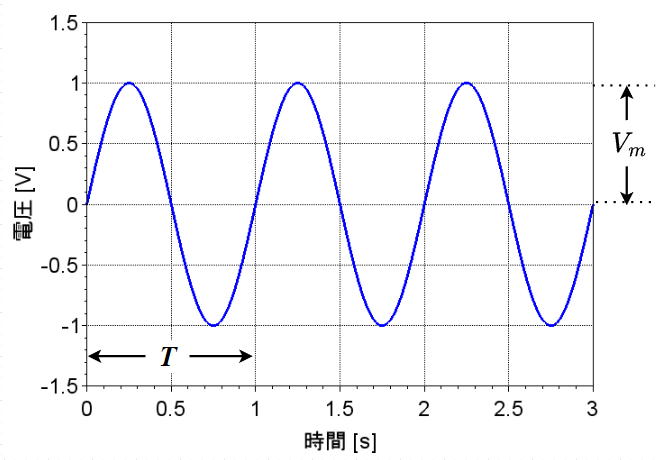
図「交流電圧波形」で、振幅\(V_m\) [V]、周期\(T\) [s]とすると、正弦波電圧波形は、$$v(t) = V_m \sin \omega t \;[V]$$と表せる。この\(v(t)\)を瞬時値という。ここで、\(\omega = 2 \pi f\) [rad/s]、\(f =1/T\) [Hz]である。

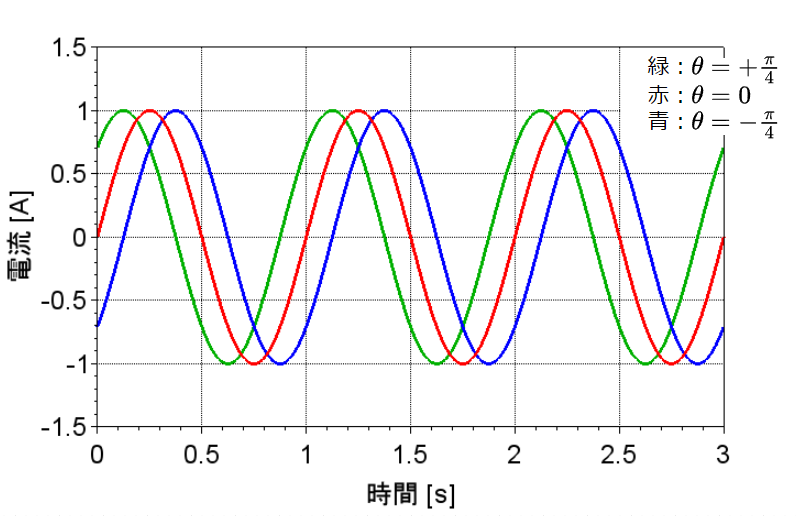
交流電流の式で位相\(\theta\)を考慮すると、$$i(t) = I_m \sin(\omega t + \theta) \; [A]$$と表せる。これをグラフにすると図「交流電流波形で位相を変化させた場合」のようになる。
図で緑線は、位相\(\theta = +\pi/4\)とした場合で、\(\pi/4\)位相進み（または、45° 位相進み）という。赤線は、位相\(\theta = 0\)とした場合で、位相零である。青線は、位相\(\theta = -\pi/4\)とした場合で、\(\pi/4\)位相遅れ（または、45° 位相遅れ）という。この場合、赤線が位相進み、位相遅れの基準となっている。
交流電圧も同様に表記でき、$$v(t) = V_m \sin(\omega t + \theta) \; [V]$$となる。
※位相を表記する場合、度数法より弧度法を使った方が便利な場合が多い。

平均値

交流電流、交流電圧の各瞬時値の絶対値の平均、または、その半周期についての各瞬時値の平均をとったものを平均値という。例えば、交流電流の平均値は、$$I_a = \frac{2}{T}\int_0^{T/2} idt=\frac{1}{\pi}\int_0^{\pi} i d\theta \;[A] $$となる。交流電流が正弦波の場合、$$I_a = \frac{1}{\pi} \int_0^{\pi} i d\theta = \frac{1}{\pi}\int_0^{\pi} I_m \sin \theta d \theta = \frac{I_m}{\pi}\left[- \cos \theta \right]_0^{\pi} = \frac{2}{\pi} I_m \; [A]$$となる。つまり、$$I_a = \frac{2}{\pi}I_m = 0.637I_m \;[A] \\ I_m = \frac{\pi}{2}I_a = 1.57 I_a \; [A]$$である。
交流電圧に関しても同様である。\(I_m\)を\(V_m\)に、単位の\([A]\)を\([V]\)に、などの変更をすればよい。$$V_a = \frac{2}{\pi}V_m = 0.637 V_m \; [V] \\ V_m = \frac{\pi}{2}V_a = 1.57 V_a \; [V]$$

実効値と最大値

実効値は、各瞬時値の二乗の平均の平方根で表される。この値は、直流と同じ電力を得られる交流をその直流の大きさで表したものである。
たとえば、交流の電熱効果を考えると、与えられた交流の実効値に等しい直流とは、同じ電熱効果を生じるように定めたものとなる。交流電流の実効値\(I\)を積分を使って表すと、$$I = \sqrt{\frac{1}{T} \int_0^T i^2 dt} \; [A]$$となる。交流電流が正弦波の場合、$$I = \sqrt{\frac{1}{T} \int_0^T i^2 dt} = \sqrt{\frac{1}{T} \int_0^T I_m^2 \sin^2 \omega t dt} \\= I_m \sqrt{\frac{1}{T} \cdot \frac{1}{2} \int_0^T (1 - \cos 2 \omega t )dt} = I_m \sqrt{\frac{1}{2} - \frac{1}{2T} \int_0^T \cos 2 \omega t dt} \\ \int_0^T\cos 2 \omega t dt = \frac{1}{\omega} \int_0^{2\pi} \cos 2 \theta d \theta = 0 $$よって、$$I = \frac{I_m}{\sqrt{2}} = 0.707 I_m\; [A]$$である。また、最大値は、\(I_m = \sqrt{2}I =1.414 I \; [A]\)となる。
交流電圧に関しても同様である。\(I_m\)を\(V_m\)に、単位の\([A]\)を\([V]\)に、などの変更をすればよい。ただし、交流電圧の実効値は\(E\)と記す。$$E = \frac{V_m}{\sqrt{2}} = 0.707 V_m \; [V]$$また、最大値は、\(V_m = \sqrt{2}E=1.414 E \; [V]\)となる。

直流電力と交流電力

抵抗\(R \; [\Omega]\)に\(i = I_m \sin \omega t \; [A]\)の正弦波電流が流れているとき、時間\(t\)の瞬間における消費電力は、$$p= R i^2 = R I_m^2 \sin^2 \omega t \; [W]$$この1周期の平均電力は、$$P = R \left(\frac{I_m}{\sqrt{2}}\right)^2 \; [W]$$となる。一方、抵抗\(R\)に直流\(I_d \; [A]\)を流したときの電力\(P_d\)は、$$P_d = R I_d^2 \; [W]$$となる。\(P = P_d\)となるためには、$$R\left(\frac{I_m}{\sqrt{2}}\right)^2 = R I_d^2 \\ I_d = \frac{I_m}{\sqrt{2}}$$でなければならない。交流電圧に関しても同様である。