27. RL並列回路、RC並列回路
並列回路
回路素子を直列にした場合、各素子を流れる電流は同じで、各素子の両端の電圧が異なる。並列にすると電圧と電流が入れ替わり、各素子には同じ電圧がかかるが、各素子に流れる電流が異なる。
\(R\)だけの並列回路
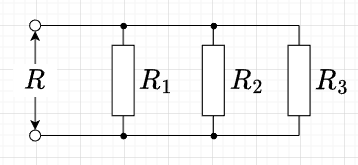
図「\(R\)だけの並列回路」のように、抵抗\(R_1, R_2, R_3\)を並列に接続した場合の合成抵抗\(R\)は直流回路の場合と同様に、$$\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \; [S]$$となる。
(※\([S] = [1/\Omega]\)である。)
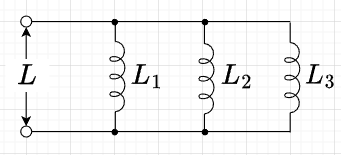
\(L\)だけの並列回路
図「\(L\)だけの並列回路」のように、インダクタ\(L_1, L_2, L_3\)を並列に接続した場合の合成インダクタンス\(L\)は、$$\frac{1}{L} = \frac{1}{L_1} + \frac{1}{L_2} + \frac{1}{L_3} \; [1/H]$$となる。両辺を\(\omega\)で割ると、$$\frac{1}{\omega L} = \frac{1}{\omega L_1} + \frac{1}{\omega L_2} + \frac{1}{\omega L_3} \; [S]$$なので、誘導性リアクタンスで表すと、$$\frac{1}{X_L} = \frac{1}{X_1} + \frac{1}{X_2} + \frac{1}{X_3} \; [S]$$である。ここで、$$X_L = \omega L\; [\Omega]$$
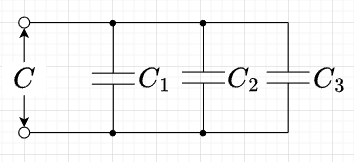
\(C\)だけの並列回路
図「\(C\)だけの並列回路」のように、キャパシタ\(C_1, C_2, C_3\)を並列に接続した場合の合成キャパシタンス\(C\)は、$$C = C_1 + C_2 +C_3 \;[F]$$となる。両辺に\(\omega\)を乗じると、$$\omega C = \omega C_1 + \omega C_2 + \omega C_3 \;[S]$$なので、容量性リアクタンスで表すと、$$\frac{1}{X_C} = \frac{1}{X_1} + \frac{1}{X_2} + \frac{1}{X_3} \; [S]$$である。ここで、$$X_C= \frac{1}{\omega C} \; [\Omega]$$
\(RL\)並列回路
図「\(RL\)並列回路」のように、抵抗\(R \;[\Omega]\)とインダクタンス\(L \; [H] \)が並列に接続された回路に\(e = E_m \sin \omega t \; [V]\)の電圧を加えた場合を考える。
ここで、振幅\(E_m \; [V]\)、実効値\(E \;[V]\)で、\(E_m = \sqrt{2}E \; [V]\)である。
抵抗には電流\(i_R\)として、$$i_R = \frac{E_m}{R} \sin \omega t \; [A]$$が、また、インダクタンスには、電流\(i_L\)として、$$i_L = \frac{E_m}{\omega L} \sin \left(\omega t - \frac{\pi}{2}\right) \; [A]$$が流れる。
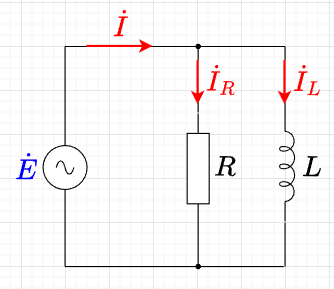
つまり、\(R\)には電圧\(\dot{E}\)と同相の電流\(\dot{I}_R\)、\(L\)には電圧\(\dot{E}\)より\(\frac{\pi}{2}\)位相遅れの電流\(\dot{I}_L\)が流れる。電源から流れ出る電流\(i\)は、\(i_R\)と\(i_L\)の和なので、$$i = i_R + i_L = \frac{E_m}{R} \sin \omega t + \frac{E_m}{\omega L} \sin \left(\omega t - \frac{\pi}{2}\right) =\frac{E_m}{Z}\sin (\omega t - \theta)$$ここで、$$Z=\frac{R \omega L}{\sqrt{R^2 + (\omega L)^2}}, \;\;\;\; \theta = \tan^{-1} \frac{R}{\omega L}$$である。よって、電流の大きさは電圧を\(Z\)で割った値になり、電流の位相は電圧より\(\theta\)だけ遅れる。ベクトル図で示すと「\(RL\)並列回路のベクトル図(電圧基準)」のようになる。
ベクトル図を参照して、ベクトルで計算すると、$$\dot{I} = \dot{I}_R + \dot{I}_L$$なので、電流の大きさは、$$I = \sqrt{{I_R}^2 + {I_L}^2} = \sqrt{\left(\frac{E}{R}\right)^2 + \left(\frac{E}{\omega L}\right)^2 } = E \frac{\sqrt{R^2 +(\omega L)^2}}{R \omega L} \; [A]$$ $$Z=\frac{E}{I} = \frac{R \omega L}{\sqrt{R^2 +(\omega L)^2}} \; [\Omega] \\ \theta = \tan^{-1} \frac{I_L}{I_R} = \tan^{-1} \frac{\frac{E}{\omega L}}{\frac{E}{R}} = \tan^{-1} \frac{R}{\omega L}$$となる。
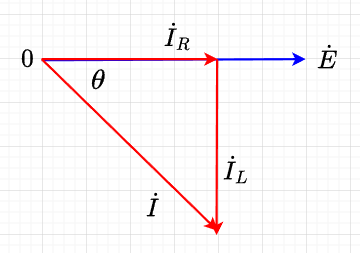
(電圧基準)
\(RC\)並列回路
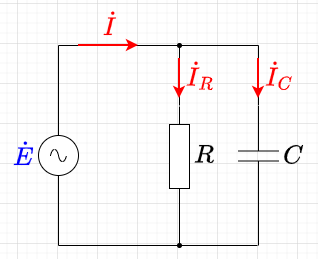
図「\(RC\)並列回路」のように、抵抗\(R \;[\Omega]\)とキャパシタンス\(C \; [F] \)が並列に接続された回路に\(e = E_m \sin \omega t \; [V]\)の電圧を加えた場合を考える。
ここで、振幅\(E_m \; [V]\)、実効値\(E \;[V]\)で、\(E_m = \sqrt{2}E \; [V]\)である。
抵抗には電流\(i_R\)として、$$i_R = \frac{E_m}{R} \sin \omega t \; [A]$$が、また、キャパシタンスには、$$i_C = \omega C E_m\sin \left(\omega t + \frac{\pi}{2}\right) \; [A]$$が流れる。
ベクトル図は、図「\(RC\)並列回路のベクトル図(電圧基準)」と表せる。このベクトル図を参照して、ベクトルで計算すると、電流の大きさは、$$I = \sqrt{{I_R}^2 + {I_C}^2} = \sqrt{\left(\frac{E}{R}\right)^2 + (\omega C E)^2} \\ = E \sqrt{\frac{1}{R^2} + (\omega C)^2} \; [A]$$ $$Z = \frac{E}{I} = \frac{1}{ \sqrt{\frac{1}{R^2} + (\omega C)^2}} \;[\Omega] \\ \theta = \tan^{-1} \frac{I_C}{I_R} = \tan^{-1} \frac{\omega C E}{\frac{E}{R}} = \tan^{-1} R \omega C$$となる。
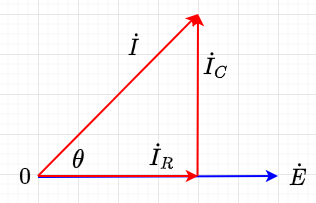
(電圧基準)

