28. RLC並列回路

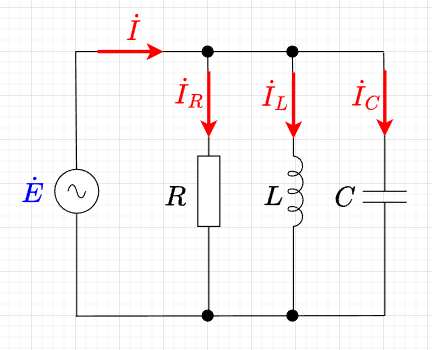
図「\(RLC\)並列回路」のように抵抗R[Ω]、インダクタンスL[H]、キャパシタンスC[F]を並列に接続した回路に\(\dot{E} \;[V]\)の電圧を加えた場合を考える。
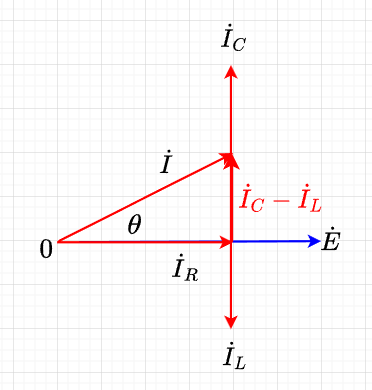
このベクトル図は、図「\(RLC\)並列回路のベクトル図」のようになる。
\(\dot{I}_C\)と\(\dot{I}_L\)は \(\pi\) の位相差があるから、\(\dot{I}_C + \dot{I}_L\)の大きさは、\(I_C - I_L\)となる。従って、全電流\(I\)の大きさは、$$I = \sqrt{{I_R}^2 + (I_C - I_L)^2} \\= \sqrt{ \left( \frac{E}{R}\right)^2 + \left(\omega CE - \frac{E}{\omega L} \right)^2} \\= E \sqrt{ \left( \frac{1}{R}\right)^2 + \left(\omega C - \frac{1}{\omega L} \right)^2} \;[A]$$となる。インピーダンス\(Z\)は、$$Z=\frac{E}{I} = \frac{1}{\sqrt{ \left( \frac{1}{R}\right)^2 + \left(\omega C - \frac{1}{\omega L} \right)^2} } \; [\Omega]$$である。また、位相は、$$\theta = \tan^{-1} \frac{(I_C - I_L)}{I_R} \\= \tan^{-1} \frac { \omega CE - \frac{E}{\omega L}}{\frac{E}{R}} \\= \tan ^{-1} R \left(\omega C - \frac{1}{\omega L} \right)$$である。
ここで、\(X = \omega C - \frac{1}{\omega L}\)として、 \(X\)の値が正であれば、全電流\(\dot{I}\)は、電圧\(\dot{E}\)より\(\theta\)だけ位相が進み、負であれば、\(\theta\)だけ位相が遅れることになる。