31. 交流回路の電力
交流の電力は、直流の電力と同様に、電圧と電流の積で求められる。交流では、電圧と電流が時間とともに変化するので、その積である電力も変化する。この電力を瞬時電力\(p\)という。$$p = v i \;[W]$$
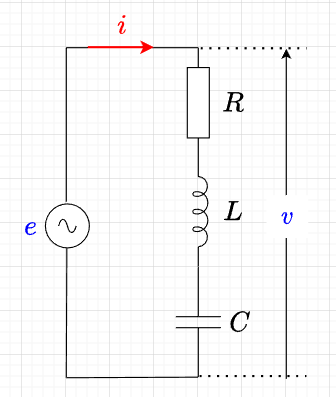
図「交流回路」で、電圧\(v \;[V]\)より電流\(i \; [A]\)が\(\phi\)だけ位相が遅れているとすると、\(v,\;i,\;p\)は$$ p = vi = V_m \sin \omega t \cdot I_m \sin (\omega t - \phi) \\= V_m I_m \sin \omega t \cdot \sin(\omega t - \phi) \\=\frac{V_m I_m }{2} \left\{\cos \phi - \cos(2 \omega t - \phi)\right\} \;[W]\;\; \cdots (1)$$ となる。ここで、この回路の平均電力\(P \;[W]\)は、瞬時電力\(p\)の1周期の平均なので、式(1)の第2項の1周期の平均値は零であるから、第1項だけの平均値$$P=\frac{V_m I_m}{2}\cos \phi = VI\cos \phi \;[W]\;\; \cdots (2)$$となる。\(V_m, \; I_m\)は振幅、\(V, \; I\)は実効値である。(\(V_m = \sqrt{2}V , \; I_m =\sqrt{2}I\))図「交流回路の電力」で以上の関係を示す。青線が電圧、赤線が電流、緑線が電力である。式(2)で表される電力を有効電力といい、単位は\([W]\)(ワット)である。式(2)から分かるように、回路の素子が抵抗\(R\)だけの場合、電圧と電流の位相差が零なので、\(\phi = 0\)で\(\cos \phi =1\)なので、\(P=VI \;[W]\)となる。
また、平均値と実効値の定義から、直流の電力\(P_{DC} = RI^2\;[W] \)と同じ式で求めることができるので、\(L, \; C\)では有効電力は消費されず、抵抗のみで消費される電力となる。
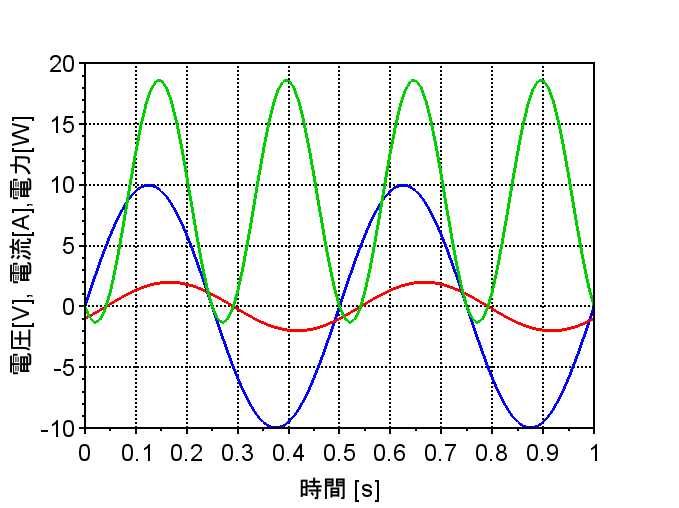
青:電圧、赤:電流、緑:電力
皮相電力と力率
有効電力の式(2)から分かるように、交流回路では、電圧\(V\)と電流\(I\)の大きさだけでは、電力\(P\)は決まらない。\(V\)と\(I\)との積は見かけ上の電力で、皮相電力という。量記号として\(P_s\)、単位には\([V\cdot A]\)(ボルトアンペア)を用いる。$$P_s = VI \; [V\cdot A]$$である。
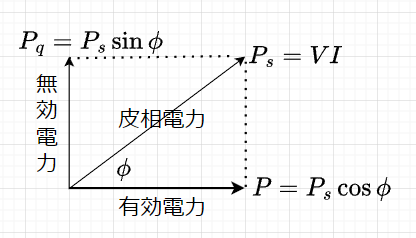
有効電力\(P\)と皮相電力の比を力率という。$$力率 = \frac{P}{P_s} = \frac{VI \cos \phi}{VI} = \cos \phi$$である。また、(\(\sin^2 \phi + \cos^2 \phi = 1\)) より、$$\sin \phi = \sqrt{1 - \cos^2 \phi}$$を無効率という。
皮相電力と無効率の積を無効電力という。量記号として\(P_q\)、単位には\([\mathrm{var}]\)(バール)を用いる。$$P_q = VI \sin \phi \;[\mathrm{var}]$$である。無効電力は、熱消費を伴わない電力である。また、\(P_s, \; P, \; P_q\)の関係は、$$P_s = \sqrt{P^2 + {P_q}^2} \;[V\cdot A]$$である。

