10. 負荷線（直流と交流）

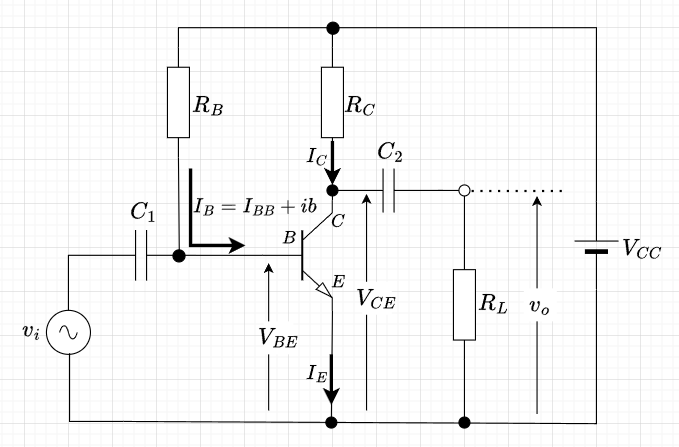
エミッタ接地増幅回路の負荷線について考える。図１は固定バイアスでのエミッタ接地増幅回路の構成例である。\(C_1,\;\; C_2\)のカップリングコンデンサにより、直流回路と交流回路に分けて考えることができる。直流回路は、\(C_1,\;\;C_2\)の部分で回路を開放にして考えれば良い。この場合、ベース電流を\(I_{BB}\)とすると、$$I_{BB} = \frac{V_{CC} - V_{BE}}{R_B}$$と表せ、入力側の動作点は(\(V_{BE},\;\;I_{BB}\)）となる。
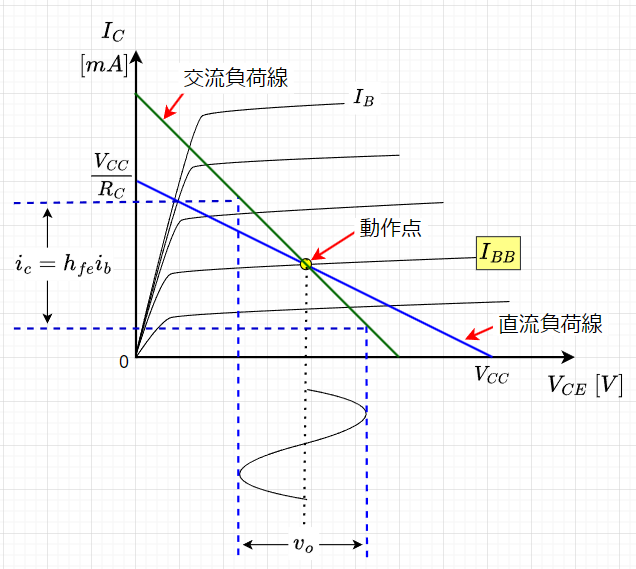
一方、出力側（コレクタ側）は、$$V_{CC} = I_C R_C + V_{CE} \\ I_C = -\frac{1}{R_C} V_{CE} + \frac{V_{CC}}{R_C}$$と表せ、これが直流負荷線の式である。 図２「直流負荷線と交流負荷線」の青線が直流負荷線である。この直流負荷線と\(I_{BB}\)におけるBJTの\(V_{CE} - I_C\)特性との交点が、出力側の動作点となる。

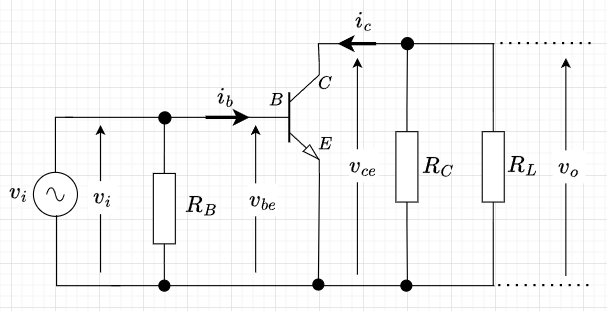
交流動作を考える場合、コンデンサと直流電源は、交流を通過させるので、図１のカップリングコンデンサ\(C_1,\;\; C_2\)と直流電源\(V_{CC}\)部分で回路を短絡させればよい。そうすると、図３「エミッタ接地増幅回路の交流回路」が得られる。この場合、入力電圧\(v_i\)がベース・エミッタ間に掛かることになる。つまり、\(v_{be} = v_i\)である。直流を含めると、\(V_{BE} + v_{be}\)となる。）
出力電圧は、\(v_{ce} = v_o\)で、\(v_o = -i_c R_{AC}\)となる。ここで、\(R_{AC}\)は\(R_C\)と\(R_L\)の並列抵抗値$$R_{AC} = \frac{R_C R_L}{R_C + R_L}$$である。従って、交流負荷線は、$$i_c= -\frac{1}{R_{AC}} v_{ce}$$のように傾き\(-\frac{1}{R_{AC}}\)で動作点を通る直線となる。図２の緑線が交流負荷線である。

入力側の動作点\(I_{BB}\)と\(V_{CE}-I_C\)特性図上の直流負荷線の交点で決まる動作点を（\(V_{CEQ},\;\;I_{CQ}\)）（図２の黄色点）とすると、交流負荷線の式は、$$I_C = -\frac{1}{R_{AC}}V_{CE} + I_{CQ} + \frac{V_{CEQ}}{R_{AC}}$$と表せる。

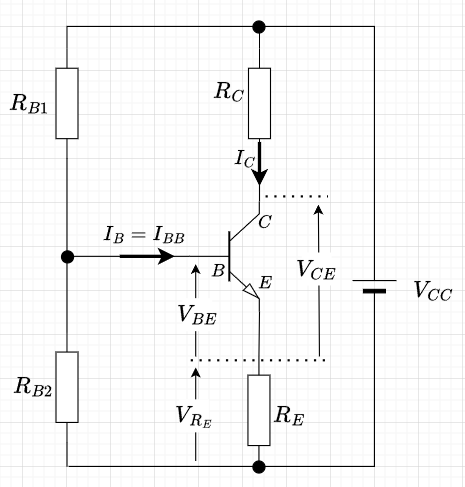
図４は、電流帰還バイアスを使ったエミッタ接地増幅回路の基本的な構成例である。直流負荷線を求めるために、直流回路を考える。図４から、コンデンサ\(C_1,\;\;C_2,\;\;C_E\)部分を開放して、直流回路を取り出す。図５が電流帰還バイアスを使ったエミッタ接地増幅回路の直流回路である。
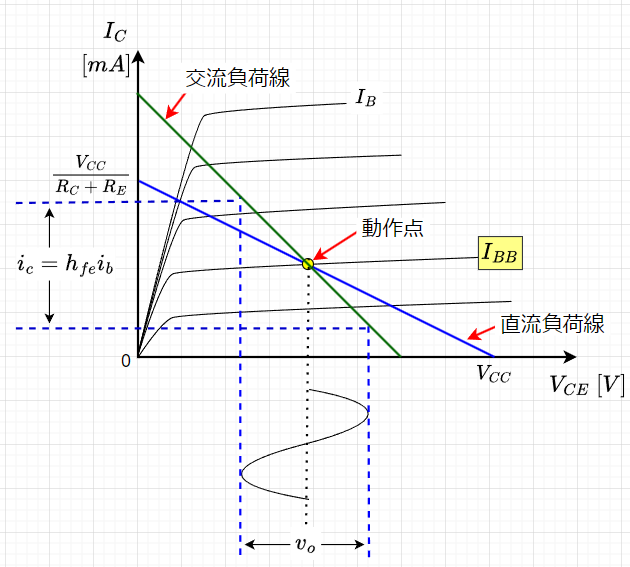
図５から、$$V_{BE} = \frac{R_{B2}}{R_{B1} + R_{B2}} V_{CC} - V_{R_E} \\ V_{R_E} = R_E I_E \approx R_E I_C \\ V_{CE} = V_{CC} - R_C I_C - V_{R_E}$$従って、直流負荷線の式は、$$I_C= -\frac{1}{R_C + R_E} V_{CE} + \frac{V_{CC}}{R_C + R_E}$$となる。図６の青線が直流負荷線である。
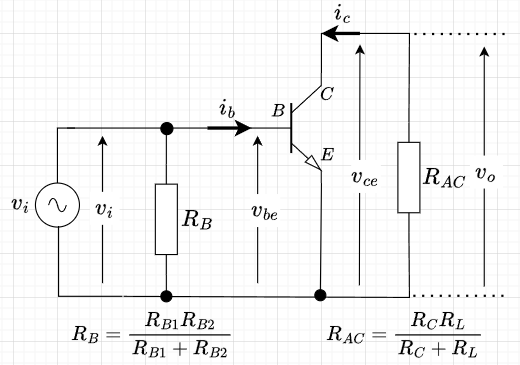
交流負荷線を考える上で、図4から交流回路を得る。コンデンサと直流電源は、交流を通過させるので、図４のカップリングコンデンサ\(C_1,\;\; C_2\)とバイパスコンデンサ\(C_E\)、及び、直流電源\(V_{CC}\)を短絡させればよい。その結果、図７「エミッタ接地増幅回路の交流回路（電流帰還バイアス）」が得られる。図７から、入力電圧\(v_i\)がベース・エミッタ間に掛かることになる。すなわち、\(v_{be} = v_i\)である。また、出力電圧は、\(v_{ce} = v_o\)であり、\(v_o = -i_c R_{AC}\)となる。ここで、\(R_{AC}\)は\(R_C\)と\(R_L\)の並列抵抗値$$R_{AC} = \frac{R_C R_L}{R_C + R_L}$$である。従って、交流負荷線は、$$i_c= -\frac{1}{R_{AC}} v_{ce}$$のように傾き\(-\frac{1}{R_{AC}}\)で動作点を通る直線となる。図６の緑線が交流負荷線である。

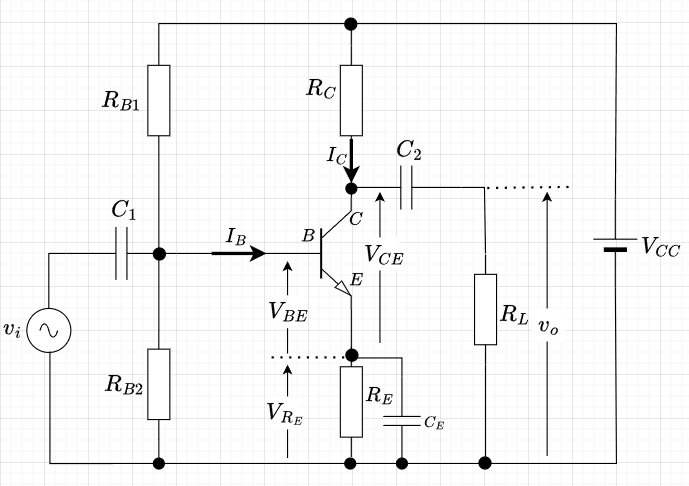
図４　エミッタ接地増幅回路（電流帰還バイアス）