11. BJTの等価回路
BJT(バイポーラトランジスタ)の等価回路とは、BJTの内部構造を単純化し、電気回路素子(抵抗、キャパシタ、インダクタ、電圧源、電流源など)で表した回路モデルである。BJTの等価回路は、大きく分けて直流等価回路と交流等価回路の2種類がある.
直流等価回路(ダイオードモデル):直流等価回路は、BJTの内部構造を2つのダイオードと電流源でモデル化したもので、このモデルでは、エミッタ-ベース接合は順方向バイアス、ベース-コレクタ接合は逆方向バイアスされていることを表現している。図1は、pnpとnpnの「BJTの直流等価回路(ダイオードモデル)」である。直流等価回路は、BJTのコレクタ電流\(I_C\)とベース電流\(I_B\)を計算するために用いられる。
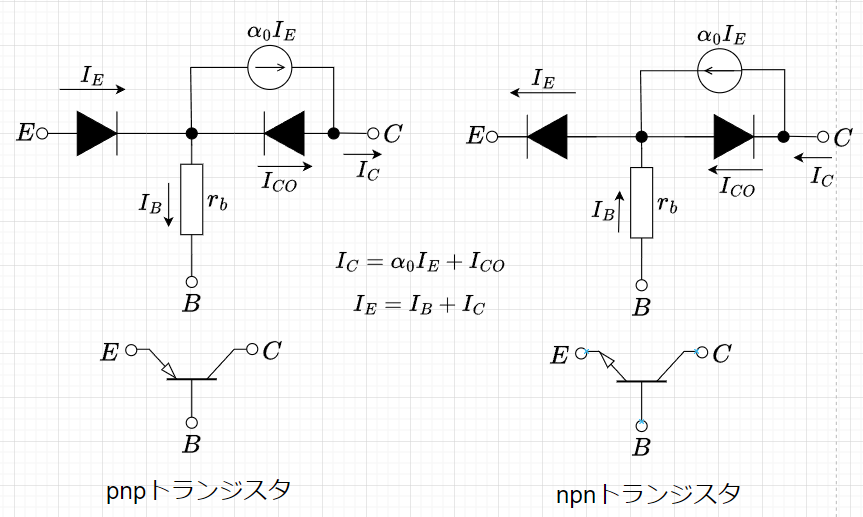
(ダイオードモデル)
交流等価回路:交流等価回路は、BJTの電圧、電流の変化分に対する動作(交流動作)をモデル化したもので、内部構造を電流源と抵抗で表す。図2がBJTの交流等価回路で、「ベース接地BJTのT形等価回路」において、\(r_e\)は、順方向バイアスダイオードの等価抵抗、\(r_c\)は、逆方向バイアスダイオードの等価抵抗である。交流等価回路では、変化分の電圧、電流の向きは自由に定めて良いためpnpトランジスタとnpnトランジスタは、 同一の交流等価回路となる。また、一般に\(0.991 \leq \alpha < 1.0\)(従って、\(\beta >100\))である。なお、交流等価回路は、主にBJTの増幅度や周波数特性を計算するために用いられる。
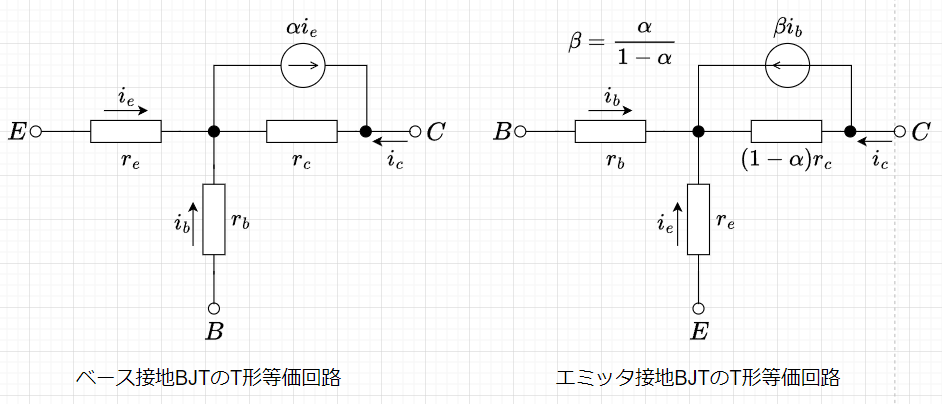
小信号等価回路:小信号等価回路は、交流等価回路の一種で、BJTの入力信号と出力信号の振幅が小さい場合に用いられる。このモデルでは、BJTの静特性から各パラメータを決定する。
図3がBJTの静特性例である。小信号での等価回路を考える場合、動作点近傍における特性の変化量をみる。
1)\(V_{CE}-I_C\)特性(出力特性):\(I_B\)を一定にした状態で、\(V_{CE}\)の変化に対する\(I_C\)の変化を測定したものである。\(V_{CE}\)がある値以上(図3の例では1V以上)では、\(V_{CE}\)を変化させても\(I_C\)はほとんど変化しない。この特性の傾きは、出力アドミタンス\(h_{oe} \;[S]\)を表している。$$h_{oe} = \frac{\Delta I_C}{\Delta V_{CE}} = \frac{i_c}{v_{ce}} \;\;\;[S]$$である。一般に小信号の増幅器としてBJTを使用する場合は、この値が小さい領域で使う。
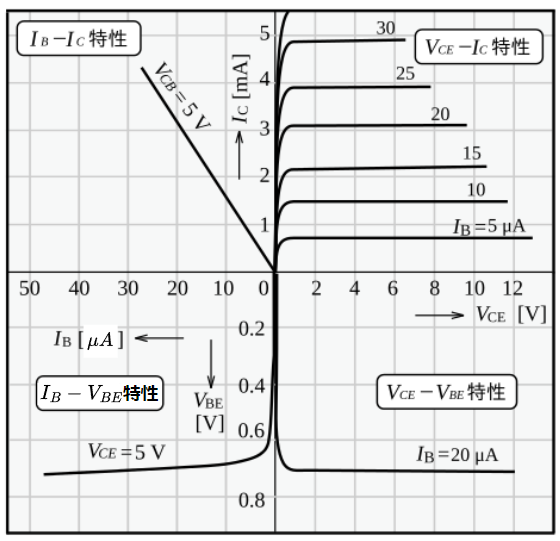
2)\(I_B - I_C\)特性(電流伝達特性):\(V_{CE}\)を一定にした状態で、\(I_B\)の変化に対する\(I_C\)の変化を測定したものである。これは、ほぼ比例関係で直線となる。この特性の傾きは、電流増幅率\(h_{fe} = \beta\)を表している。$$h_{fe} = \frac{\Delta I_C}{\Delta I_B} = \frac{i_c}{i_b}$$である。
3)\(I_B - V_{BE}\)特性(入力特性):\(V_{CE}\)を一定にした状態で、\(V_{BE}\)の変化に対する\(I_B\)の変化を測定したものである。\(V_{BE}-I_B\)特性として用いることが多い。この特性の傾きは、入力インピーダンス\(h_{ie} \; [\Omega]\)を表している。$$h_{ie} = \frac{\Delta V_{BE}}{\Delta I_B} = \frac{v_{be}}{i_b} \;\;\; [\Omega]$$である。
4)\(V_{CE} - V_{BE}\)特性(電圧帰還率):\(I_B\)を一定にした状態で、\(V_{CE}\)の変化に対する\(V_{BE}\)の変化を測定したものである。この特性の傾きは、電圧帰還率\(h_{re}\)を表している。$$h_{re} = \frac{\Delta V_{BE}}{\Delta V_{CE}} = \frac{v_{be}}{v_{ce}}$$である。一般的に、図3から分かるように、この値は非常に小さい。
hパラメータによる小信号等価回路(エミッタ接地)
図3の静特性において、動作点近傍における各特性の傾き(小信号の変動に伴う特性の変化)を基にして、小信号等価回路を考えることができる。ここでは、エミッタ接地でのhパラメータによる小信号等価回路を示す。hパラメータを使うと、小信号入力\(v_{be}\)に対する出力\(i_c\)を以下の式で表せる。$$\left \{ \begin{aligned}
& v_{be} = h_{ie} i_b + h_{re} v_{ce} \\ & i_c = h_{fe} i_b + h_{oe} v_{ce} \end{aligned} \right.$$これらの式を回路図で表すと図4の小信号等価回路のようになる。さらに、多くの場合、$$ h_{re} v_{ce} \ll h_{ie} i_b \;\;\;\;\; h_{oe} v_{ce} \ll h_{fe} i_b $$なので、$$\left \{ \begin{aligned} & v_{be} = h_{ie} i_b \\ & i_c = h_{fe} i_b \end{aligned} \right.$$と簡略化できる。
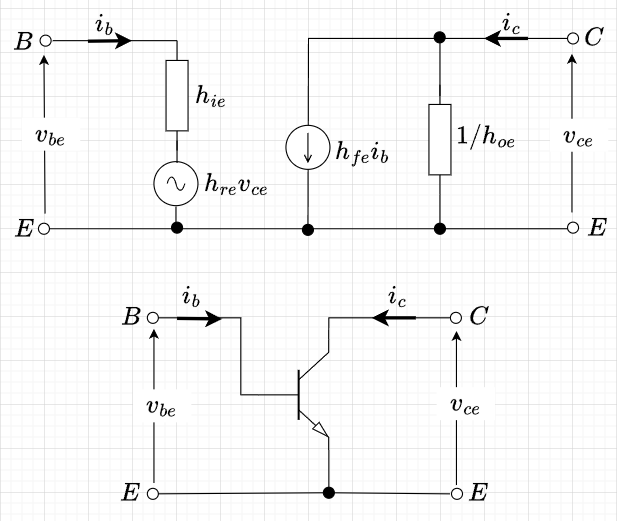
(エミッタ接地)
簡易等価回路
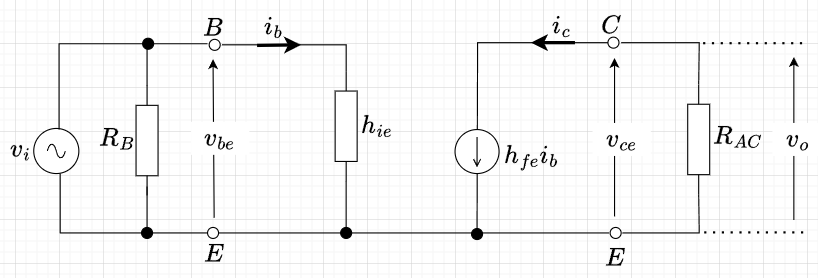
このBJTの簡易等価回路を使って、「10. 負荷線(直流と交流)の図7」に示す「エミッタ接地増幅回路の交流回路」を簡易小信号等価回路で表すと図5「エミッタ接地増幅回路の簡易等価回路」となる。図5から次の式が得られる。$$i_b = \frac{v_i}{h_{ie}} \\ v_o = - i_c R_{AC} = -h_{fe} i_b R_{AC} = -h_{fe} \frac{v_i}{h_{ie}} R_{AC}$$従って、電圧増幅度\(A_v\)は、$$A_v = \frac{v_o}{v_i} = -\frac{h_{fe}}{h_{ie}}R_{AC}$$となる。また、電流増幅度\(A_i\)は、$$A_i = \frac{i_c}{i_b} = \frac{h_{fe} i_b}{i_b} = h_{fe}$$となる。さらに、電力増幅度\(A_p\)は、$$A_p = \frac{-i_c v_o}{i_b v_i} = \frac{(-h_{fe} i_b)(-h_{fe} \frac{v_i}{h_{ie}} R_{AC})}{i_b v_i} = \frac{h_{fe}^2}{h_{ie}} R_{AC}$$となる。

