18. 負帰還増幅回路
負帰還増幅回路とは、出力の一部を入力に戻すことによって、増幅回路の利得や周波数特性などの特性を改善する回路で、増幅回路と帰還回路から構成される。帰還回路は、出力端子から出力された信号を、入力端子に戻す回路である。
負帰還増幅回路の利点は、以下の4点にまとめられる。
(1)利得の安定化:一般に増幅回路の開放利得は、温度や電源電圧などの影響で変化する。負帰還増幅回路では、帰還回路によって、入力端子と出力端子間の電圧差を一定に保つように働く。そのため、増幅回路の開放利得の変化の影響を抑えることができる。
(2)非線形歪みの低減:増幅回路の歪みは、入力信号の波形を歪ませる可能性がある。負帰還増幅回路では、帰還回路によって、入力端子と出力端子間の電圧差を一定に保つように働き、増幅回路の歪みの影響を抑えることができる。
負帰還増幅回路は、電子回路の基本的な要素であり、非常に重要な役割を果たしている。
(3)周波数特性の改善:増幅回路の周波数特性は、入力インピーダンスや出力インピーダンスなどの特性によって影響を受ける。負帰還増幅回路では、帰還回路によって、入力インピーダンスや出力インピーダンスを一定に保つように働き、そのため、増幅回路の周波数特性を改善することができます。
(4)ノイズの抑制:増幅回路のノイズは、入力信号に影響を与える可能性がある。負帰還増幅回路では、帰還回路によって、入力端子と出力端子間の電圧差を一定に保つように働く。そのため、増幅回路のノイズの影響を抑えることができる。
負帰還増幅回路の原理
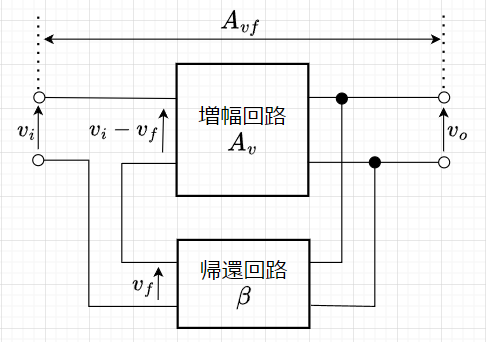
図1は負帰還増幅回路の原理図である。増幅回路\(A_v\)と帰還回路\(\beta\)から構成される。増幅回路の出力の一部を入力側へ逆位相になるよう戻している。これを負帰還という。図1で、\(v_o\)が出力電圧、\(v_f\)が帰還電圧で、その比が帰還率\(\beta\)である。$$\beta = \frac{v_f}{v_o}$$従って、\(v_f = \beta v_o\)である。
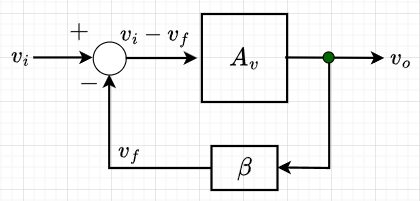
図2は、図1を基に制御工学で良く使うブロック線図で描いた負帰還増幅回路の構成図である。図2(または、図1)より、$$v_o = A_v(v_i - v_f) \;\;\;\;\; v_f = \beta v_o$$である。この2式より、負帰還がかかった電圧増幅度は、$$A_{vf} = \frac{v_o}{v_i} = \frac{A_v}{1 + \beta A_v}$$となる。
また、$$A_{vf} = \frac{1}{\frac{1}{A_v} + \beta}$$なので、増幅回路だけの増幅度\(A_v\)が非常に大きい場合、$$ A_{vf} = \lim_{A_v \rightarrow \infty} \frac{1}{\frac{1}{A_v} + \beta} = \frac{1}{\beta} \\ v_o = \frac{v_i}{\beta}$$である。つまり、帰還率\(\beta\)の逆数が、負帰還増幅回路の電圧増幅度となる。ここで、\(\beta A_v\)を開ループゲイン、\(A_{vf}\)を閉ループゲインという。
負帰還の利点
利得の安定化
利得\(A_v\)の変動が\(A_{vf}\)に及ぼす影響を考える。$$A_{vf} = \frac{A_v}{1 + \beta A_v}$$の両辺の対数をとり\(A_v\)で微分する。両辺の対数をとると$$\log{A_{vf}} = \log {\frac{A_v}{1 + \beta A_v}} $$である。この両辺をそれぞれ微分すると、$$\frac{1}{A_{vf}} \frac{d A_{vf}}{d A_v} = \frac{\frac{1 + \beta A_v -\beta A_v}{(1 + \beta A_v)^2}}{\frac{A_v}{1 + \beta A_v}} \\ = \frac{1}{1 + \beta A_v} \frac{1}{A_v} $$ となる。これは、次のように書き直せる。$$\frac{\Delta A_{vf}}{A_{vf}} = \frac{1}{1 + \beta A_v} \frac{\Delta A_v}{A_v}$$つまり、増幅回路の増幅度\(A_v\)の変動\(\Delta A_v\)の影響が、\(\frac{1}{1 + \beta A_v}\)に抑制される。
非線形ひずみの低減
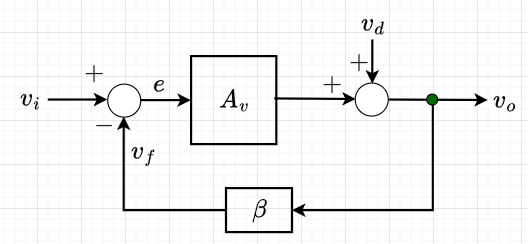
増幅回路を構成する電子素子であるトランジスタの利得は非線形で、入力信号の振幅に依存する。このため、出力信号は歪みを生じる。この歪み成分を\(v_d\)として、図3のように増幅回路\(A_v\)の出力に加算されたものと考えると、この歪みを生じた出力信号は$$v_o = A_v e + v_d \; , \;\;\;\; e= v_i - v_f \; , \;\;\;\; v_f = \beta v_o$$と表せる。
よって、$$v_o = A_v (v_i - \beta v_o ) + v_d\;\; , \;\;\;\;\;\;\;\;\;\;\; v_o(1 + \beta A_v ) = A_v v_i + v_d \\ v_o = \frac{A_v}{1 + \beta A_v} v_i + \frac{1}{1 +\beta A_v} v_d$$となる。つまり、歪み成分\(v_d\)は、\(\frac{1}{1 + \beta A_v}\)に低減されることになる。
なお、\(v_d\)をノイズ\(v_n\)と置き換えれば、同様の議論が成り立つので、ノイズ\(v_n\)も、\(\frac{1}{1 + \beta A_v}\)に抑制されることになる。
周波数特性の改善
高域の遮断周波数を\(f_h\)とすると、増幅度\(A_v\)は、$$A_v = \frac{A_0}{1 + j \frac{\omega}{\omega_h}} \;\;\;\; \cdots (1) \\ \omega_h = 2 \pi f_h$$と表せる。ここで、\(A_0\)は中域の増幅度とする。
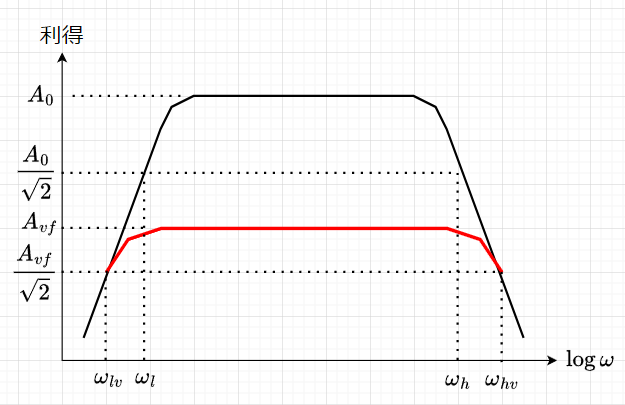
負帰還を掛けると、\(A_{vf} = \frac{A_v}{1 + \beta A_v}\)になるので、(1)式を代入すると、$$A_{vf} = \frac{ \frac{A_0}{1 + j \frac{\omega}{\omega_h}}}{1 + \beta \frac{A_0}{1 + j \frac{\omega}{\omega_h}}} \\ = \frac{A_0}{1 + j \frac{\omega}{\omega_h} + \beta A_0} = \frac{A_0}{1 + \beta A_0} \frac{1}{1 + j \frac{\omega}{\omega_h(1 + \beta A_0)}}$$となる。このように、遮断周波数\(\omega_h\)が\(\omega_{hv}=\omega_h (1 + \beta A_0)\)となり、\((1 + \beta A_0)\)倍になる。低域の遮断周波数も同様に考えられる。以上より、図4「負帰還による周波数特性の改善」のように、高域の遮断周波数\(\omega_h\)も低域の遮断周波数\(\omega_l\)も、\(\omega_{hv} , \;\; \omega_{lv}\)と広がる。
負帰還回路の種類
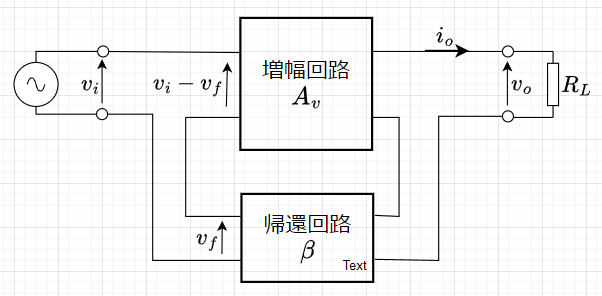
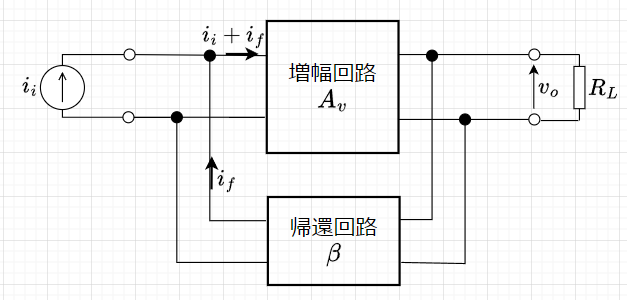
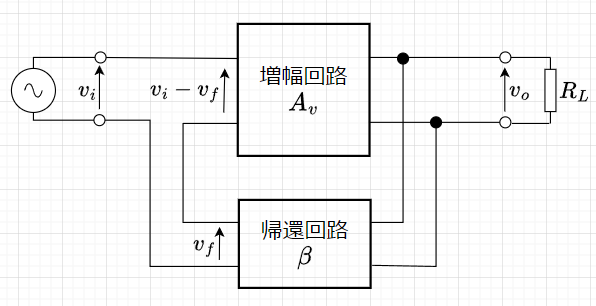
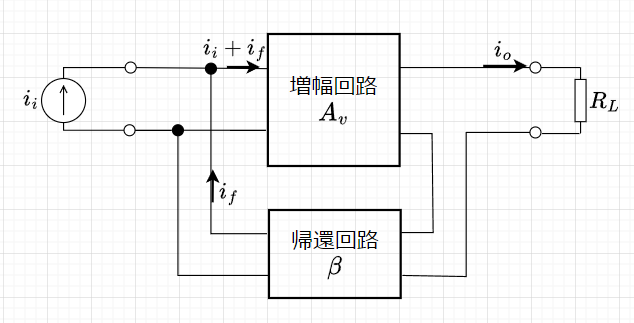
負帰還の掛け方には、図5、図6、図7、図8のように、入力側で直列帰還、並列帰還、出力側で直列帰還、並列帰還があるので、計4種類の帰還方法がある。
負帰還回路における入出力インピーダンス
入力インピーダンス
図6の「直列ー並列帰還」を使った増幅回路の等価回路は、図9のようになる。図9より、$$v_o = \frac{R_L}{Z_o + R_L} A_v v_e \approx A_v v_e \\ v_e = v_i - v_f = v_i - \beta v_o \\ i_i = \frac{v_e}{Z_i}$$となる。(一般に、増幅回路\(A_v\)の出力インピーダンス\(Z_o\)は負荷抵抗\(R_L\)に比べて十分小さい)
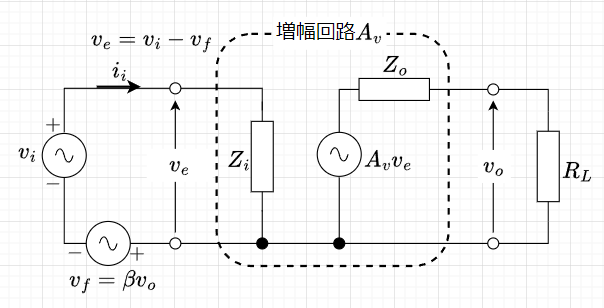
入力インピーダンス計算用
従って、入力インピーダンスは、$$Z_{in} = \frac{v_i}{i_i} = \frac{v_e + \beta v_o}{i_i} = \frac{v_e + \beta A_v v_e}{i_i} = (1 + \beta A_v) \frac{v_e}{i_i} =(1 +\beta A_v) Z_i$$となる。つまり、信号源\(v_i\)からみた入力インピーダンスは、負帰還が掛かる前の増幅回路の入力インピーダンス\(Z_i\)の\((1 + \beta A_v)\)倍になる。
出力インピーダンス
出力インピーダンスを求めるには、入力信号源\(v_i\)を短絡して、負荷抵抗\(R_L\)の代わりに信号源\(v_o\)を接続して、出力インピーダンスを計算する。図10より、$$i_o = \frac{v_o - A_v v_e}{Z_o} \\ v_e = -v_f = - \beta v_o$$となる。
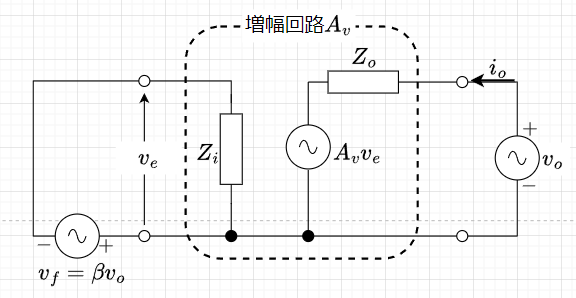
出力インピーダンス計算用
従って、出力インピーダンスは、$$Z_{out} = \frac{v_o}{i_o} = \frac{Z_o v_o}{v_o - A_v v_e} = \frac{Z_o v_o}{v_o + \beta A_v v_o} = \frac{1}{1 + \beta A_v} Z_o$$となる。つまり、出力端からみた出力インピーダンスは、負帰還が掛かる前の増幅回路の出力インピーダンス\(Z_o\)の\(\frac{1}{1 + \beta A_v}\)になる。

