19. エミッタフォロワ(コレクタ接地増幅回路)
エミッタフォロワ(Emitter Follower)とは、バイポーラトランジスタを使った基本的な増幅回路構成の1つであり、電圧利得が1で入力電圧に従って出力電圧が変化する。エミッタフォロワの動作では、ベースに印加された入力電圧がエミッタに追従する。エミッタがベースの信号をフォローするため、「エミッタフォロワ」と呼ばれる。電界効果トランジスタで構成される同等の増幅回路はドレイン接地回路と呼ぶ。この回路は信号を増幅(電流増幅)するだけでなく、入力と出力の間のインピーダンスを変換するのに役立つ。
エミッタフォロワの特徴として、・入力信号と出力信号は同位相、・入力インピーダンスが比較的高い、・出力インピーダンスが低いため負荷の影響を受けにくい、・電圧利得が1であるため出力信号の波形が歪みにくい、などがある。
エミッタフォロワの動作
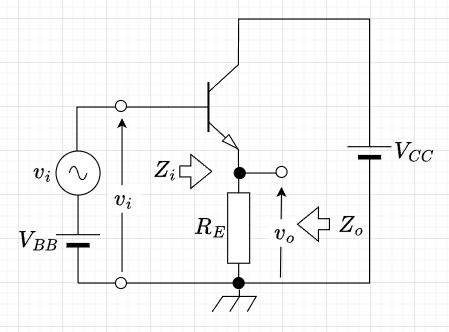
図1がエミッタフォロワ(コレクタ接地増幅回路)である。コレクタ接地増幅回路では、エミッタ接地増幅回路において\(R_C = 0\)として、さらに出力電圧\(v_o\)を\(R_E\)の両端から取り出し、帰還電圧\(v_f\)を出力電圧\(v_o\)と等しくした回路である。\(v_i = v_o + V_{BE}\)で、\(V_{BE} \approx 0.7 \; V\)なので、出力電圧\(v_o\)は入力電圧\(v_i\)にほとんど等しく従う(follow)という意味でエミッタフォロワと呼ばれている。
電圧増幅度
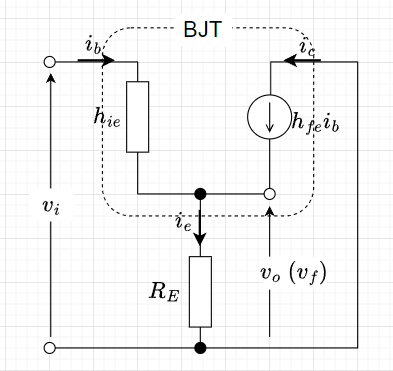
図2は、図1の回路図でBJTを\(h\)定数を使って書き換えた、交流の簡易等価回路である。交流等価回路なので、直流定電圧源(\(V_{CC} , \; V_{BB}\))部分を短絡している。図2より、入力電圧\(v_i\)は、$$i_e = i_b + i_c \;,\;\;\;\;i_c = h_{fe} i_b \\ v_i = h_{ie} i_b + R_E i_e = h_{ie} i_b + (1 + h_{fe}) i_b \;\;\;\cdots (1)$$となり、出力電圧\(v_o\)は、$$v_o = R_E ( 1 + h_{fe}) i_b$$となる。従って、電圧増幅度\(A_{vf}\)は、$$A_{vf} = \frac{v_o}{v_i} = \frac{R_E ( 1 + h_{fe}) }{h_{ie} + (1 + h_{fe}) }$$である。一般に、\(R_E( 1 + h_{fe}) \gg h_{ie}\)が成立するので、$$A_{vf} \approx 1 $$となる。
入力インピーダンス
入力インピーダンス\(R_i\)は、式(1)から$$R_i = \frac{v_i}{i_b} = h_{ie} + R_E( 1 + h_{fe}) \approx h_{ie} + h_{fe} R_E \\ (h_{fe} >100)$$である。
いま、\(R_E = 1 \; k\Omega\)、BJTを2SC1815Y(\(h_{fe} : 160\;,\;\; h_{ie} : 3.5\;k\Omega\))とした場合、$$R_i = 3.5 + 160 \times 1 = 163.5 \; k\Omega$$となり、\(h_{ie}\)の値よりかなり大きくなる。
出力インピーダンス
図1において、出力端子に何も接続していない時の出力電圧(開放電圧)を\(v_o\)とし、出力端子を短絡したときに出力端子に流れる電流(短絡電流)を\(i_s\)とすると、テブナンの定理より、$$i_s = \frac{v_o}{Z_o} ,\;\;\;\; Z_o = \frac{v_o}{i_s}$$となる。図2において、開放電圧\(v_o\)は、\(A_{vf} \approx 1\)より、\(v_o = A_{vf} v_i \approx v_i\)となる。短絡電流\(i_s\)は、\(R_E\)を短絡するので、\(R_E=0\)として、$$i_s = i_e = i_b + i_c = (1 + h_{fe}) i_b =(1 + h_{fe})\frac{v_i}{h_{ie}}$$である。従って、出力インピーダンス\(Z_o\)は、$$Z_o = \frac{v_o}{i_s} = \frac{v_i}{(1 + h_{fe})\frac{v_i}{h_{ie}}} = \frac{h_{ie}}{1 + h_{fe}} \approx \frac{h_{ie}}{h_{fe}}$$となる。
BJTを2SC1815Y(\(h_{fe} : 160\;,\;\; h_{ie} : 3.5\;k\Omega\))とした場合、$$Z_o = \frac{h_{ie}}{h_{fe}} \approx 22 \; \Omega$$と、\(Z_o\)は小さい値となる。
テブナンの定理
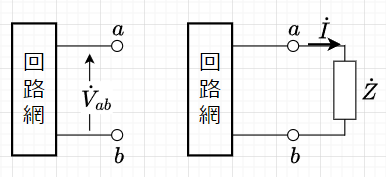
図3に示すように、ある回路網中の2端子を\(a,\;b\)として、\(ab\)間の開放端電圧を\(\dot{V}_{ab}\)とする。この2端子間にインピーダンス\(\dot{Z} \; [\Omega]\)を図3右のように接続した場合、\(\dot{Z}\)に流れる電流\(\dot{I}\)は、$$\dot{I} = \frac{\dot{V}_{ab}}{\dot{Z}_o+ \dot{Z}}$$となる。ここで、\(\dot{Z}_o\)は、回路網中のすべての起電力を除いて、\(a,\;b\)端子からみた回路網中の合成インピーダンスである。 以上をテブナンの定理という。
詳しくは、16. テブナンの定理(基礎電気回路)を参考にしてください。
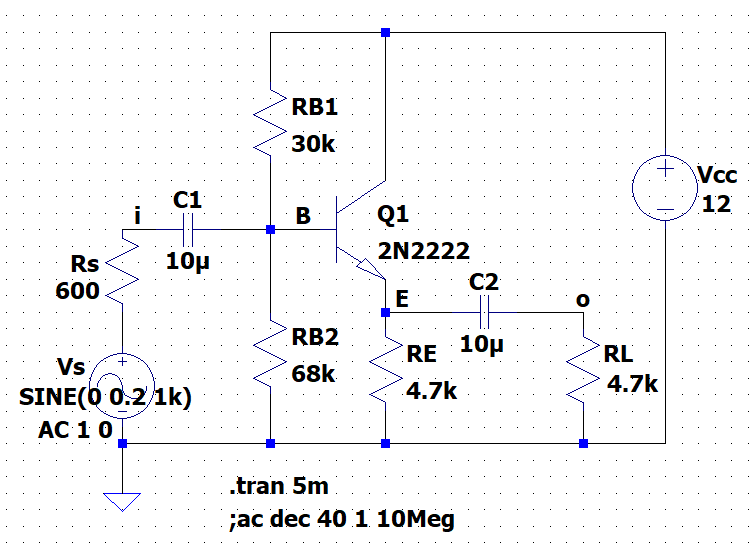
エミッタフォロワ(LTspice)
図4は、エミッタフォロワのLTspice用回路図である。ベース電圧は、$$V_B \approx \frac{RB2}{RB1 + RB2} V_{CC} = 8.3 \; V$$である。従って、エミッタ電圧\(V_E\)は、$$V_E = V_B - V_{BE} \approx 7.6 \; V $$である。(\(V_{BE} = 0.7 \;V\)としている。) 入力信号\(V_s\)は、振幅0.2 V、周波数 1 kHzの正弦波である。
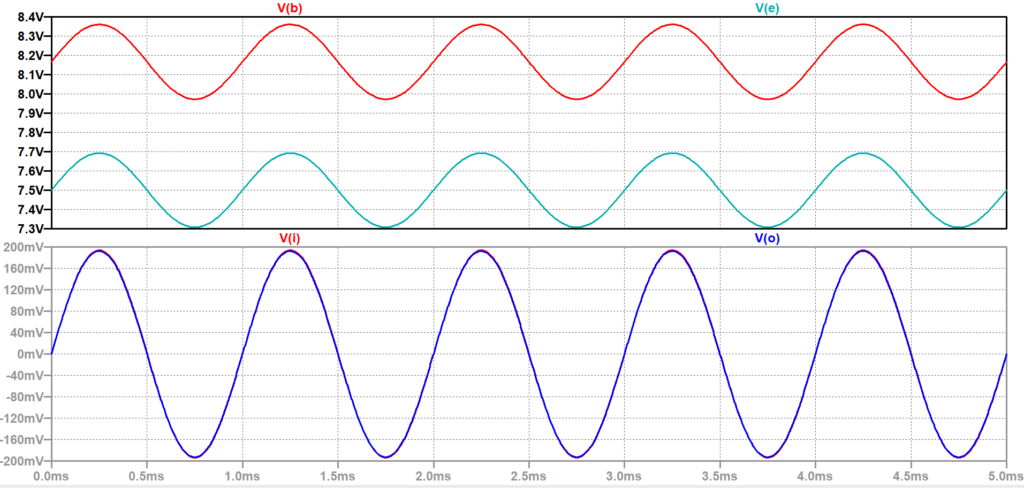
図5がシミュレーション結果である。\(V_i\)と\(V_o\)は同相で同振幅となっており、エミッタフォロワの動作となっている。ベース電圧\(V_b\)とエミッタ電圧\(V_e\)は、同波形で\(V_{BE}\)分だけベース電圧\(V_b\)がエミッタ電圧\(V_e\)より高くなっている。