20. 電流帰還直列注入形負帰還増幅回路
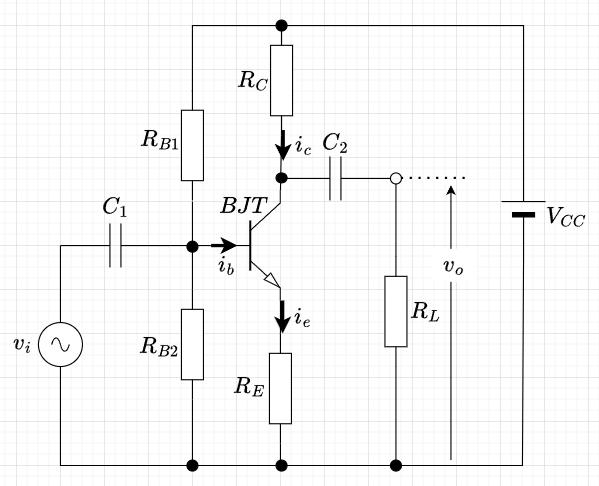
図1に電流帰還直列注入形負帰還増幅回路を示す。この回路は、CR結合増幅回路において、エミッタのバイパスコンデンサを取り外した構成となっている。CR結合増幅回路では、エミッタの抵抗は電流帰還バイアスとして働いている。そして増幅度を落とさないようにエミッタにバイパスコンデンサを取り付けている。バイパスコンデンサを取り外し、エミッタ抵抗\(R_E\)を交流信号に対しても使うことで、負帰還増幅回路となる。ただし、全体の増幅度は低下することになる。
図1より、出力電流のコレクタ電流\(i_c\)が増加すると、\(i_e = i_c + i_b \approx i_c\)なので、エミッタ電流\(i_e\)が増加する。その結果、\(R_E\)による電圧降下\(R_E i_e\)が大きくなり、エミッタ電圧\(v_e\)が高くなる。この\(v_e\)が帰還電圧となり、\(v_{be} = v_b - v_e\)なので、\(v_{be}\)が低下するので、\(i_b\)が減少し、その結果、\(i_c = h_{fe} i_b\)が減少する。つまり、負帰還がかかったことになる。
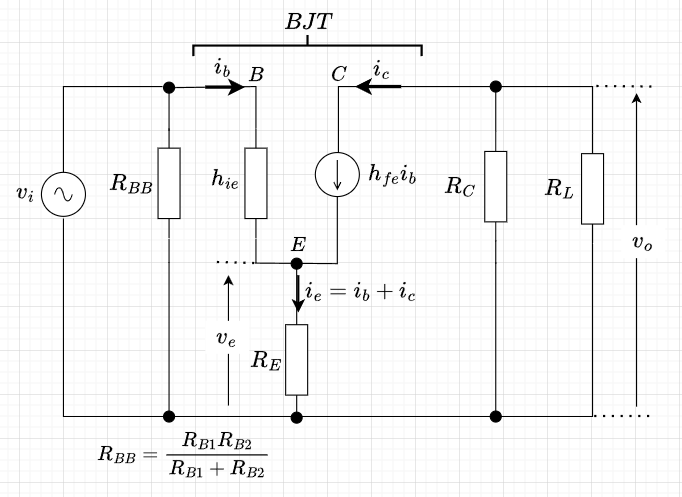
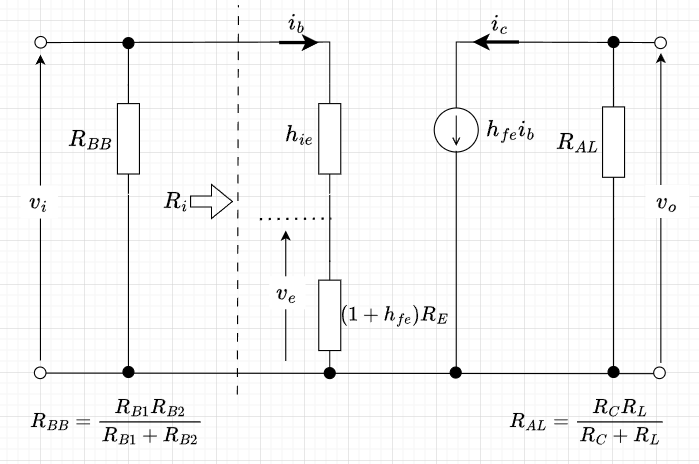
図2の等価回路より、$$v_e = R_E(i_b + h_{fe} i_b) = R_E (1 + h_{fe}) i_b $$ $$v_i = h_{ie} i_b + v_e = h_{ie} i_b + R_E (1 + h_{fe}) i_b \\= \left\{ h_{ie} + R_E (1 + h_{fe})\right\} i_b \\ \approx (h_{ie} + h_{fe} R_E) i_b $$である。また、図3より、$$v_o = -i_c R_{AL} = -h_{fe} i_b R_{AL}$$となる。ここで、\(R_{AL}\)は\(R_C\)と\(R_L\)の並列合成抵抗である。$$R_{AL} = \frac{R_C R_L}{R_C + R_L}$$
以上より、増幅度\(A_{vf}\)は、$$ A_{vf} = \frac{v_ o}{v_i} = \frac{v_o}{i_b} \frac{i_b}{v_i} =-\frac{h_{fe} i_b R_{AL}}{i_b} \frac{i_b}{(h_{ie} + h_{fe} R_E) i_b} \\ = -\frac{h_{fe} R_{AL}}{(h_{ie} + h_{fe} R_E)} = -\frac{h_{fe} R_{AL}}{h_{ie} \left( 1+ \frac{h_{fe}}{h_{ie}} R_E \right)} = A_v \frac{1}{1 + \frac{h_{fe}}{h_{ie}} R_E} = \frac{A_v}{1 - \frac{R_E}{R_{AL} }A_v} \\= \frac{A_v}{1 - \beta A_v}\;\;\; \cdots (1) $$となる。ここで、\(A_v\)は、負帰還が掛かる前の増幅度、つまり\(R_E=0\)での増幅度で、$$A_v = - \frac{h_{fe} R_{AL}}{h_{ie}}$$である。なお、増幅度の負号(\(-\))は、入力に対して出力が逆相であることを示している。また、\(\beta\)は帰還率で、$$\beta = \frac{R_E}{R_{AL}}$$である。
(1)式より、\(A_v\)が十分に大きい場合、$$ \frac{A_v}{1 - \beta A_v} = \frac{1}{\frac{1}{A_v} - \beta} \rightarrow -\frac{1}{\beta} = -\frac{R_{AL}}{R_E}$$となり、増幅度\(A_{vf}\)は、抵抗比で求まる。
図3より、ベースから見た入力抵抗\(R_i\)は、$$R_i = \frac{v_i}{i_b} = h_{ie} + h_{fe}R_E = h_{ie} ( 1 - \beta A_v)$$となる。
電流帰還直列注入形負帰還増幅回路(LTspice)
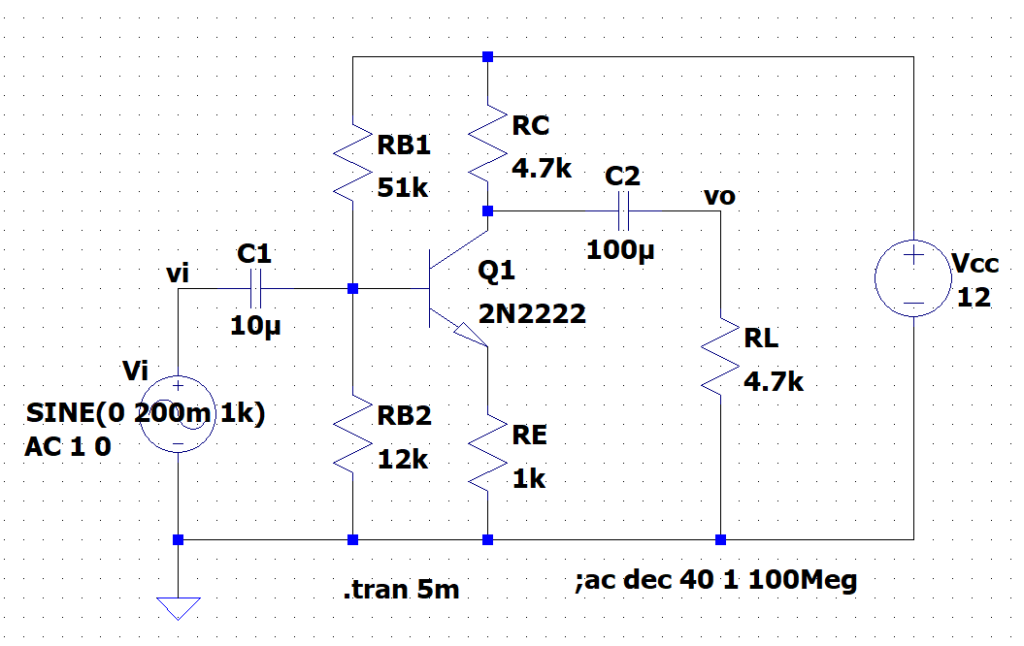
図4は、電流帰還直列注入形負帰還増幅回路のLTspice用回路図である。入力信号\(v_i\)は、振幅 200 mV, 周波数 1 kHzの正弦波としている。負荷抵抗値\(R_{AL}\)は、\(R_C\)と\(R_L\)の並列抵抗値なので、\(R_{AL} = 2.35 \;k \Omega\)で、\(R_E = 1\; k \Omega\)より、増幅度\(A_{vf}\)は、$$A_{vf} \approx -\frac{R_{AL}}{R_E} = 2.35$$となる。
図5がシミュレーション結果で、\(v_i\)の振幅 200 mVに対して、\(v_o\)の振幅は 465 mVとなっており、増幅度\(A_{vf}\)の概算値と良い一致を示している。また、\(v_i\)と\(v_o\)は逆相となっている。
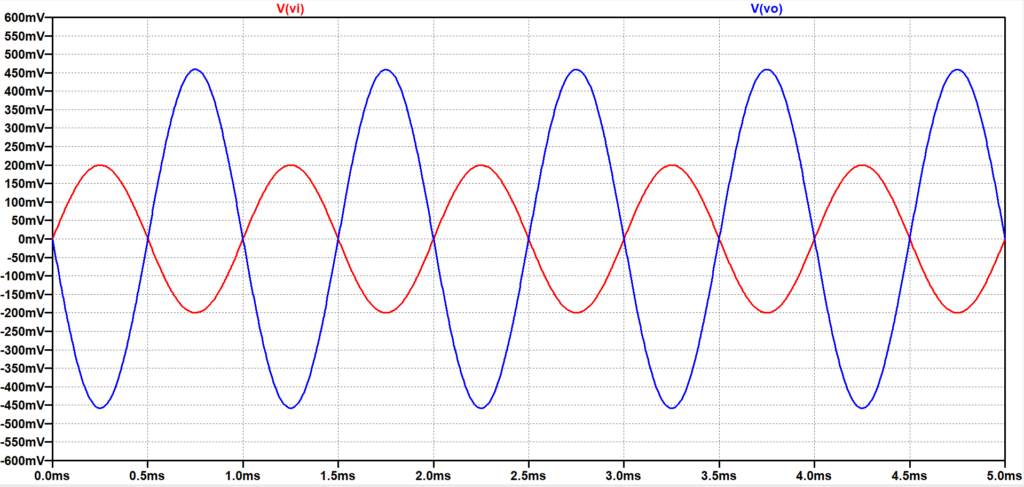
赤:入力信号\(v_i\)、青:出力信号\(v_o\)

