27. LC発振回路
LC発振回路は、インダクタンス\(L\)とキャパシタンス\(C\)を使用して振動を生成する発振回路である。LC回路は、共振周波数と呼ばれる特定の周波数で振動し、この共振周波数は、LとCの値によって決まる。一般的に、このタイプの発振回路は、周波数安定性が高いために広く使用されている。
LC発振回路の動作原理
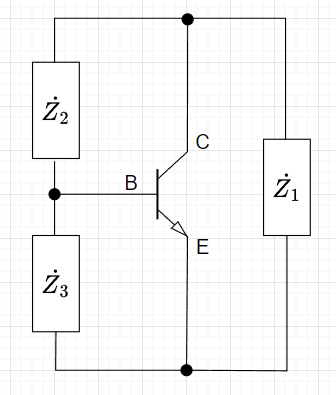
図1は、LC発振回路の一般形である三素子型発振回路の交流回路(バイアスを除いた交流部分の回路)である。トランジスタの三端子間にリアクタンス\(\dot{Z_1},\;\dot{Z_2},\;\dot{Z_3}\)を接続して構成された発振回路である。
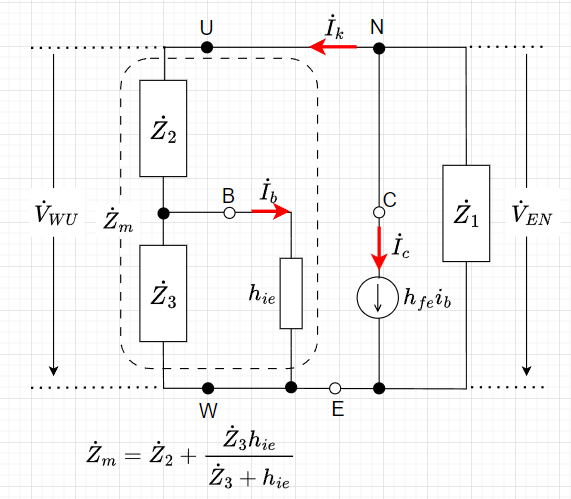
図2は、三素子型発振回路の小信号等価回路である。図にあるように、各線間電圧、各線電流をベクトルで表示する。図より、端子E-N間の電圧\(\dot{V}_{EN}\)は、$$\dot{V}_{EN} = \dot{I}_c \frac{\dot{Z}_1 \dot{Z}_m}{\dot{Z}_1 + \dot{Z}_m}$$また、このとき\(\dot{V}_{WU}\)は、$$\dot{V}_{WU} = -\dot{I}_k \dot{Z}_m$$であり、\(\dot{V}_{EN} = \dot{V}_{WU}\)なので、$$\dot{I}_c \frac{\dot{Z}_1 \dot{Z}_m}{\dot{Z}_1 + \dot{Z}_m} = - \dot{I}_k \dot{Z}_m$$また、$$\dot{Z}_m = \dot{Z}_2 + \frac{\dot{Z}_3 h_{ie}}{\dot{Z}_3 + h_{ie}}$$なので、$$\dot{I}_k = -\dot{I}_c \frac{\dot{Z}_1}{\dot{Z}_1 + \dot{Z}_2 + \frac{\dot{Z}_3 h_{ie}}{\dot{Z}_3 + h_{ie}}}$$となる。
また、分流の法則により、$$\dot{I}_b = \frac{\dot{Z}_3}{\dot{Z}_3 + h_{ie}}\dot{I}_k$$従って、$$\dot{I}_b = -\frac{\dot{Z}_3}{\dot{Z}_3 + h_{ie}} \frac{\dot{Z}_1}{\dot{Z}_1 + \dot{Z}_2 + \frac{\dot{Z}_3 h_{ie}}{\dot{Z}_3 + h_{ie}}}\dot{I}_c$$となる。よって、電流帰還率\(F_i = \frac{\dot{I}_b}{\dot{I}_c}\)は、$$F_i = - \frac{\dot{Z}_1 \dot{Z}_3} {h_{ie} (\dot{Z}_1 + \dot{Z}_2 + \dot{Z}_3) + \dot{Z}_3 (\dot{Z}_1 + \dot{Z}_2)}$$である。トランジスタの電流増幅率は\(h_{fe}\)で正の値であるから、発振条件は、$$h_{fe} F_i = 1$$である。よって、$$h_{fe} F_i = - h_{fe} \frac{\dot{Z}_1 \dot{Z}_3} {h_{ie} (\dot{Z}_1 + \dot{Z}_2 + \dot{Z}_3) + \dot{Z}_3 (\dot{Z}_1 + \dot{Z}_2)} = 1 \\ h_{ie} (\dot{Z}_1 + \dot{Z}_2 + \dot{Z}_3) + \dot{Z}_3 (\dot{Z}_1 + \dot{Z}_2) = -h_{fe} \dot{Z}_1 \dot{Z}_3$$である。\(\dot{Z}_1, \; \dot{Z}_2, \; \dot{Z}_3\)が純リアクタンスであるとし、\(j X_1, \; j X_2, \; j X_3\)とすると、$$h_{ie}(jX_1 + jX_2 + jX_3) + j X_3(jX_1 + jX_2) = -h_{fe}jX_1\times jX_3 \\ -X_1 X_3 - X_2 X_3 + jh_{ie}(X_1 + X_2 +X_3) = h_{fe} X_1 X_3$$となる。この式が成立するためには、実部と虚部がそれぞれ等しい必要があるので、$$X_1 + X_2 + X_3 = 0 \\h_{fe} = - \frac{X_1 +X_2}{X_1} = \frac{X_3}{X_1}$$となる。\(h_{fe}>0\)であるから、\(X_1\)と\(X_3\)は同符号となるリアクタンス素子でなければならない。また、\(X_2\)は異符号となるリアクタンス素子でなければならない。以上より、\(\dot{Z}_1\)と\(\dot{Z}_3\)は同じ種類のリアクタンス素子、\(\dot{Z}_2\)は異なるリアクタンス素子でなければならない。
ハートレー形発振回路
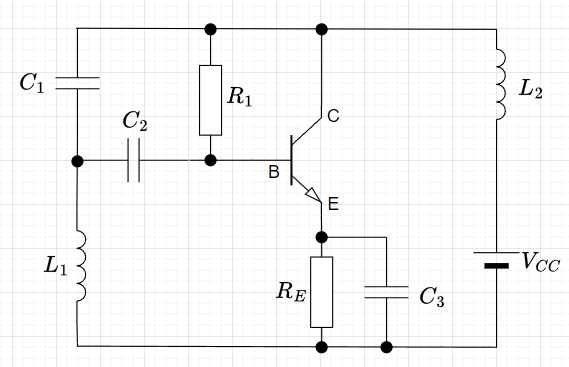
図3は、「ハートレー形発振回路」の例である。\(R_1, \; R_E\)はバイアス回路で、増幅回路はエミッタ接地増幅回路の構成となっている。\(C_2\)はカップリングコンデンサ、\(C_3\)はバイパスコンデンサで、それぞれのリアクタンスが、発振周波数に影響しないようにキャパシタンス(静電容量)を選択する。
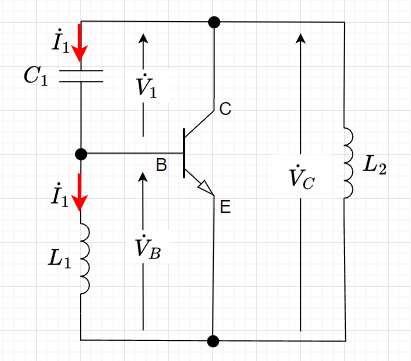
図4は、バイアス回路を除いた「ハートレー形発振回路の交流回路」である。図1に照らし合わせると、$$\dot{Z}_1 = j\omega L_2 \\ \dot{Z}_2 = \frac{1}{j \omega C_1} \\ \dot{Z}_3 = j\omega L_1$$である。従って、$$\dot{V}_1 = \frac{1}{j \omega C_1} \dot{I}_1 = -j \frac{1}{\omega C_1}\dot{I}_1 \\ \dot{V}_B = j \omega L_1 \dot{I}_1$$となる。ここで、\(\frac{1}{\omega C_1} > \omega L_1\)ならば、出力電圧\(\dot{V}_C\)が\(\frac{1}{\omega C_1}\)と\(\omega L_1\)で分圧され、\(|\dot{V}_1|\)のほうが\(|\dot{V}_B|\)より大きくなる。
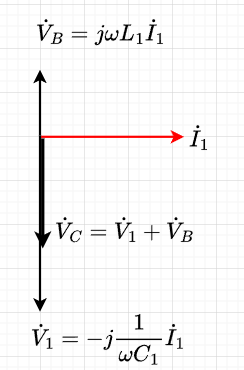
図5は、「ハートレー形発振回路のベクトル図」である。\(\dot{I}_1\)を基準ベクトル(赤線)にすると、\(\dot{V}_1\)は\(\dot{I}_1\)より90度位相遅れ、\(\dot{V}_B\)は\(\dot{I}_1\)より、90度位相進みになる。つまり、\(\dot{V}_1\)と\(\dot{V}_B\)は逆相になる。また、\(\dot{V}_C = \dot{V}_1 + \dot{V}_B\)なので、\(\dot{V}_B\)と\(\dot{V}_C\)は逆相になる。増幅回路は、エミッタ接地増幅回路なので、入力のベース電圧と出力のコレクタ電圧とは逆相である。つまり、増幅回路で逆相になり、さらに帰還回路で\(\dot{V}_B\)と\(\dot{V}_C\)は逆相になるので、結局、最初のベース入力電圧とベース電圧として帰還される電圧\(\dot{V}_B\)は同相になり、発振状態が成立する。
発振周波数は、\(L_1\)と\(L_2\)に結合が無いとすると、$$X_1 + X_2 + X_3 = \omega L_1 + \omega L_2 - \frac{1}{\omega C_1} = 0$$の関係から、$$\omega ^2 C_1(L_1 + L_2)=1 \\f = \frac{1}{2 \pi \sqrt{C_1(L_1 + L_2)} }\;\;[Hz]$$となる。


“27. LC発振回路” に対して1件のコメントがあります。
コメントは受け付けていません。