3. 論理関数と真理値表
論理関数は、入力の論理値(真または偽)を別の論理値に対応付ける規則または演算である。論理関数は通常、論理演算子(AND、OR、NOTなど)を使用して表現される。真理値表は、論理関数のすべての可能な入力の組み合わせに対する出力の値を示す表であり、各行は異なる入力の組み合わせを表し、対応する列にはその入力に対する出力が示される。
真理値表は論理関数の動作表とも言え、論理回路の設計では、真理値表から論理関数を合成し、その結果から論理回路を作製する。
各種論理関数
論理変数を\(A,\;B\)の2変数としたときの論理関数の真理値表を表1に示す。
| \(A\) | \(B\) | \(A+B\) OR | \(A \cdot B\) AND | \(\overline{A+B}\) NOR | \(\overline{A \cdot B}\) NAND | \(A \oplus B\) EXOR | \(\overline{A \oplus B}\) XNOR |
| 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
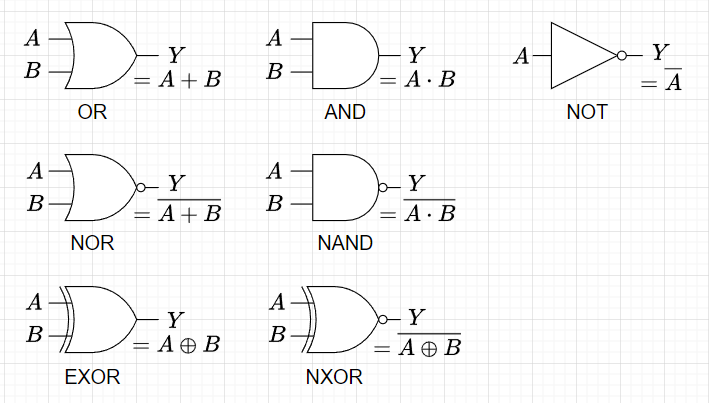
図1は、各種論理関数の回路図記号である。
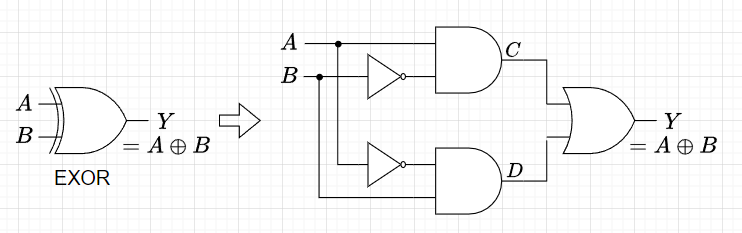
図2は、EXORをAND,OR,NOTで構成できることを示している。表2にその真理値表を示す。また、この出力\(Y\)を否定すれば、NXORとなる。
| \(A\) | \(B\) | \(C\) | \(D\) | \(Y\) |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 0 |
論理式の演算順序
論理式の演算順序は、通常、以下の順序に従う。
1)括弧内の演算:先に括弧内の演算を行う。括弧は演算の優先順位を指定するために使用され、括弧内の演算が他の演算よりも優先される。
2)論理否定 (NOT):次に、論理否定(NOT演算)を適用する。
3)論理積 (AND) および論理和 (OR):AND演算とOR演算は、一般的に左から右へ順に適用する。ただし、括弧によって指定された部分式はその中で評価する。
4)論理積 (AND) よりも論理和 (OR) の方を優先する:もしAND演算とOR演算が同じ式に混在している場合、通常はAND演算をOR演算よりも優先する。しかし、括弧が使用されていれば、その中の演算を優先する。
5)比較演算子:等しいかどうかを比較する演算子(例:\(=\))なども、他の演算子と同様に評価する。比較演算子は通常、論理積や論理和よりも後に評価されることがあるが、括弧によって指定された部分式はその中で評価する。
このような演算順序に従うことで、論理式を適切に評価できる。ただし、括弧を使用して演算順序を明示的に指定することもできるので、式を解釈し易いように括弧を適切に活用することが望ましい。
論理式の演算例
$$Y = A + \overline{A} = 1 \;\; \cdots (1)$$
| \(A\) | \(\overline{A}\) | \(Y\) |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
$$Y=A + A \cdot B = A \cdot(1 + B) =A \;\;\cdots (2)$$
| \(A\) | \(B\) | \(A \cdot B\) | \(Y\) |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 |
$$Y = A + \overline{A} \cdot B \\= A + A \cdot B + \overline{A} \cdot B \\= A + B \cdot (A+ \overline{A}) \\= A + B \;\; \cdots (3)$$
| \(A\) | \(B\) | \(\overline{A} \cdot B\) | \(A + \overline{A} \cdot B\) | \(A + B\) |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 |
$$Y = B \cdot (\overline{A} + C) + \overline{A \cdot B} \\= B \cdot \overline{A} + B \cdot C + \overline{A} + \overline{B} \\= \overline{A} \cdot (B + 1) + B \cdot C + \overline{B} \\= \overline{A} + B \cdot C + \overline{B} \\= \overline{A} + B \cdot C + (\overline{B} + \overline{B} \cdot C) \\= \overline{A} + C \cdot (B + \overline{B} ) + \overline{B} \\= \overline{A} + \overline{B} + C$$

