12. エンコーダとデコーダ
エンコーダとデコーダは、どちらも論理回路の一種で、エンコーダは、入力された信号を別の形式の符号に変換する回路であり、デコーダは符号化された信号をもとの信号に逆変換する回路である。
・エンコーダ:エンコーダは、入力された信号を別の形式の符号に変換する回路で、例えば、10進数を2進数に変換したり、文字コードをバイナリに変換したりするために使われる。
・デコーダ:デコーダは、符号化された信号をもとの信号に逆変換する回路で、例えば、2進数を10進数に変換したり、バイナリを文字コードに変換したりするために使われる。
エンコーダとデコーダは、キーボードやタッチパネルなどの入力装置等、さまざまな電子機器やシステムで広く使われている。キーボードで数字キーを押すと、エンコーダによってその数字に対応する2進数に変換され、この2進数は、コンピュータの内部で必要な処理が行われる。このように、エンコーダとデコーダは、デジタル機器の基本的な構成要素として欠かせない回路である。
ここでは、基本的なエンコード回路、デコーダ回路を例を挙げて説明する。
エンコーダ回路
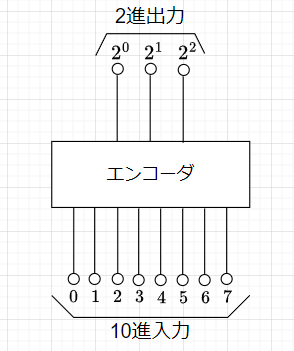
エンコーダの基本的な回路である10進-2進エンコーダを考える。回路構成の外観は、図1のようになる。
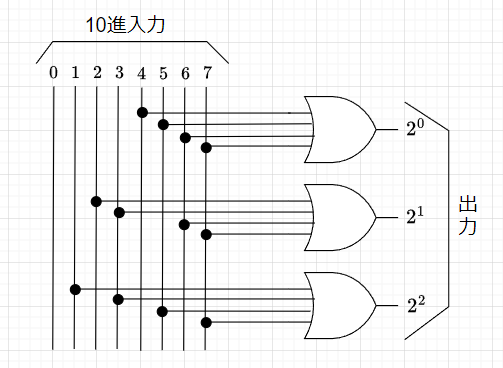
10進から2進へのエンコーダは、10進数のデータを2進数のデータに変換する。具体的には、10進数の0から7の8つの数字について、8入力(A0、A1、A2、A3、A4、A5、A6、A7)のいずれか1つが値1をとるとして、それらの2進数に対応する3ビットの出力(B2、B1、B0)を生成するエンコーダを考える。例えば、A1=1ならば、(B2、B1、B0)=(0、0、1)、A7=1ならば、(B2、B1、B0)=(1、1、1)を得る。これを表1のように8入力3出力の真理値表として作成し、それに基づいて論理回路を実現すると図2のようになる。
| A0 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | B2(\(2^2\)) | B1(\(2^1\)) | B0(\(2^0\)) |
| H | L | L | L | L | L | L | L | L | L | L |
| L | H | L | L | L | L | L | L | L | L | H |
| L | L | H | L | L | L | L | L | L | H | L |
| L | L | L | H | L | L | L | L | L | H | H |
| L | L | L | L | H | L | L | L | H | L | L |
| L | L | L | L | L | H | L | L | H | L | H |
| L | L | L | L | L | L | H | L | H | H | L |
| L | L | L | L | L | L | L | H | H | H | H |
デコーダ回路
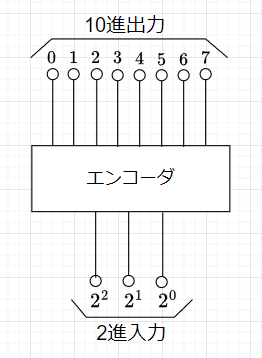
デコーダの基本的な回路である2進-10進デコーダを考える。回路構成の外観は、図3のようになる。
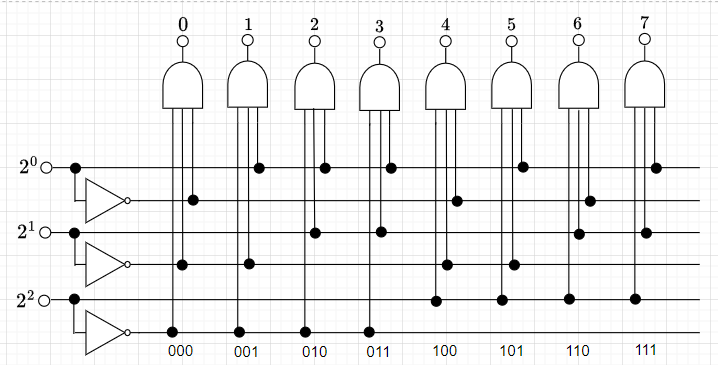
2進から10進へのデコーダは、2進数のデータを10進数のデータに変換する。具体的には、2進数の3ビットの入力(B2、B1、B0)(000から111の2進数)から、8つの出力(A0、A1、A2、A3、A4、A5、A6、A7)のいずれか1つが値1を出力するデコーダを考える。例えば、(B2、B1、B0)=(0、0、1)ならば、A1=1、(B2、B1、B0)=(1、1、1)ならば、A7=1を得る。これを表2のように3入力8出力の真理値表として作成し、それに基づいて論理回路を実現すると図4のようになる。
| B2(\(2^2\)) | B1(\(2^1\)) | B0(\(2^0\)) | A0 | A1 | A2 | A3 | A4 | A5 | A6 | A7 |
| L | L | L | H | L | L | L | L | L | L | L |
| L | L | H | L | H | L | L | L | L | L | L |
| L | H | L | L | L | H | L | L | L | L | L |
| L | H | H | L | L | L | H | L | L | L | L |
| H | L | L | L | L | L | L | H | L | L | L |
| H | L | H | L | L | L | L | L | H | L | L |
| H | H | L | L | L | L | L | L | L | H | L |
| H | H | H | L | L | L | L | L | L | L | H |

