4. LTIシステム

LTI（Linear Time-Invariant）システムとは、線形時不変システムの略称で、線形性と時不変性を満たすシステムを指し、以下の特徴を持つ。
・線形性（Linearity）：入力信号の線形結合が、出力信号においても同様に線形であるという性質を指す。
・時不変性（Time-Invariance）：システムの特性が時間に依存しないという意味である。システムの応答は、時間が経過しても変わらない。例えば、同じ入力信号を異なる時間に与えても、対応する出力信号は同じであるという性質である。
・因果性（Causality）：出力が対応する入力が発生した後のみ影響を受け、未来の入力は現在の出力に影響を与えないという性質である。
・線形時不変微分方程式の表現：LTIシステムは通常、線形時不変微分方程式でモデル化される。この方程式は、入力信号とその導関数（時間に関する微分）を用いて、出力信号を表現する。
LTIシステムはこれらの特性によって定義され、これらの特性によってシステムの解析や設計が分かりやすくなる。LTIシステム理論は、信号処理、通信、制御工学などの多くの応用分野で活用されている。

線形システム

システムが線形のとき、図１に示すように線形演算子\(L\)を用いて式(1)のように表す。$$L\left\{x(t)\right\} = y(t) \; \cdots (1)$$

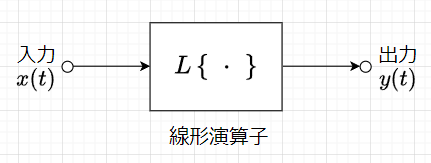
線形システムは、重ね合わせの理（重畳の理）によって定義される。入力\(x_1(t) , \; x_2(t)\)の出力を\(y_1(t), \; y_2(t)\)とすると任意の定数\(a, \; b\)に対して、$$L\left\{a x_1(t) + b x_2(t)\right\} = L \left\{a x_1(t)\right\} + L \left\{b x_2(t)\right\} = a y_1(t) + b y_2(t)$$が成り立つとき、このシステムを線形システムという。
入力\(x(t)\)に対する出力\(y(t)\)のシステムに入力\(x(t - t_0)\)を加えたとき、$$L\left\{x(t - t_0)\right\} = y(t - t_0)$$の関係が成立するシステムを時不変という。線形性と時不変性をあわせもったシステムを線形時不変（LTI）システムという。
線形システムに単位インパルス\(\delta(t)\)を入力として加えたときの応答（単位インパルス応答）を\(h(t)\)とすると、線形システムが時不変とすると、$$L \left\{ \delta (t - t_0) \right\} = h(t - t_0)$$が成り立つ。
有限な入力\(x(t)\)に対して、出力\(y(t)\)が有限であるとき、そのシステムは安定であるという。LTIシステムの安定条件として、時間領域において、インパルス応答\(h(t)\) が時間とともに 0 に収束 するならば、そのシステムは 安定 であり、\(h(t)\) が発散や振動し続けるならば、そのシステムは 不安定 である。システムが安定であれば、インパルス応答\(h(t)\)に対する条件として、$$\int_{-\infty}^{\infty} |h(t)|dt < \infty$$が成り立つ。
システムに入力が印可される前には出力が現れないこと、すなわち、\(t<0\)で、入力\(x(t)=0\)であれば、その出力も\(y(t)=0\)となるとき、そのシステムは因果性を有しているという。また、因果システムのインパルス応答は、$$h(t)=0, \;\;\; t<0$$を満たす。

畳み込み積分

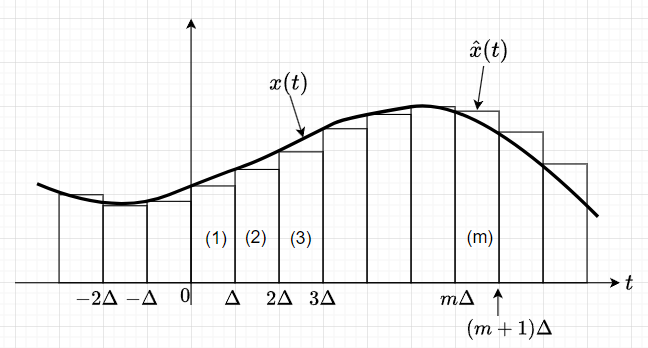
図２に連続時間信号\(x(t)\)を階段状波形\(\hat{x}(t)\)で近似するイメージを示す。$$\delta_{\Delta}(t) = \begin{cases} \frac{1}{\Delta} , \enspace 0 \leq t < \Delta \\0, \enspace その他　\end{cases}$$を定義すると、\(\Delta \cdot \delta_{\Delta}(t)\)は単位１の面積なので、図２における(1)は、\(x(0) \cdot \delta_{\Delta}(t) \cdot \Delta\)と表せるが、\(\Delta \cdot \delta_{\Delta}(t)=1\)なので、\(x(0)\)となる。同様に(2)は、\(x(\Delta) \cdot \delta_{\Delta}(t - \Delta) \cdot \Delta = x(\Delta)\)であり、(m)は、\(x(m\Delta) \cdot \delta_{\Delta}(t - m\Delta) \cdot \Delta = x(m\Delta)\)となる。従って、$$\hat{x}(t) = \sum_{k=-\infty}^{\infty} x(k \Delta)\cdot \delta_{\Delta}(t - k \Delta) \cdot \Delta \;\cdots \cdots (2)$$と表せる。\(\Delta \rightarrow 0\)で式(2)の左辺は、\(x(t)\)となる。また、右辺の\(\delta_{\Delta}(t)\)は、\(\delta_{\Delta}(t) \rightarrow \delta(t)\)となり、総和は積分に換えられるので、$$x(t) = \int_{-\infty}^{\infty} x(\tau)\delta(t - \tau) d\tau$$となる。（厳密性を無視して表現すると、\(x(t)\)は、\(\hat{x}(t)\)で\(\Delta \rightarrow 0\)としたインパルス列の集合で表せるということ。）
LTIシステムへ信号\(x(t)\)を印可したときの出力\(y(t)\)を考える。まず、\(\hat{x}(t)\)の微小パルス入力に対する応答出力を求め、それらの総和から\(\hat{y}(t)\)を求める。システムの時不変性から入力\(\delta_{\Delta}( t - k \Delta)\)に対する応答として、\(h_{\Delta}( t - k \Delta)\)を定義すると、線形性から重ね合わせの理により、出力\(y(t)\)は、$$y(t) = \lim_{\Delta \rightarrow 0} \sum_{k=-\infty}^{\infty} x(k \Delta) \cdot h_{\Delta}( t - k \Delta) \cdot \Delta$$と表せる。\(\Delta \rightarrow 0\)の極限で\(\delta_{\Delta}(t - k \Delta)　\rightarrow \delta(t- \tau) \)となり、\(h_{\Delta}( t - k\Delta) \)は、\(h_{\Delta}( t - k\Delta) \rightarrow h(t - \tau)\)のように単位インパルス応答となる。従って、右辺の総和は積分に置き換わり、$$y(t) = \int_{-\infty}^{\infty} x(\tau) h(t - \tau) d\tau \; \cdots (3)$$が得られる。これを畳み込み積分という。
インパルス応答\(h(t)\)のLTIシステムに入力\(x(t)\)を印可したときの出力\(y(t)\)は、式(3)の畳み込み積分で与えられるが、これを$$y(t) = x(t) \ast h(t)$$と表記する。