6-1. 畳み込み積分のラプラス変換
畳み込み積分(Convolution Integral)は、制御工学、信号処理、画像処理などの分野でよく使われる数学的な操作である。畳み込みは、2つの関数を組み合わせて新しい関数を生成する操作となっている。2つの連続関数\(f(t) \; g(t)\)の畳み込みは、\(\ast\)記号を使って、\(f(t) \ast g(t)\)と表記する。また、畳み込み積分のラプラス変換は、それぞれの関数のラプラス変換の積となる。$$\mathcal{L} \{ f(t) \ast g(t) \} = F(s)G(s), \;\;\;\;\; F(s)=\mathcal{L}\{f(t)\} , \;\; G(s) = \mathcal{L} \{g(t)\}$$
畳み込み積分
2つの連続関数\(f(t)\) と \(g(t)\) の畳み込み積分は、$$f(t) \ast g(t) = \int_{-\infty}^{\infty} f(\tau) g(t - \tau) d\tau$$で定義される。ここで、“\(\ast\)”は畳み込み演算子を表す。畳み込み積分は、\(g(t)\) を時間軸に沿って平行移動しながら\(f(t)\)に重ねて足し合わせた結果を表している。なお、積分範囲は関数の定義域に依存する。
任意の入力信号に対する出力信号
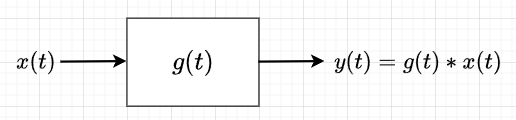
図1に示すように、インパルス応答が\(g(t)\)の線形要素に任意の入力信号\(x(t)\)が印可された時の出力信号\(y(t)\)は、$$y(t) = g(t) \ast x(t)$$で表せる。
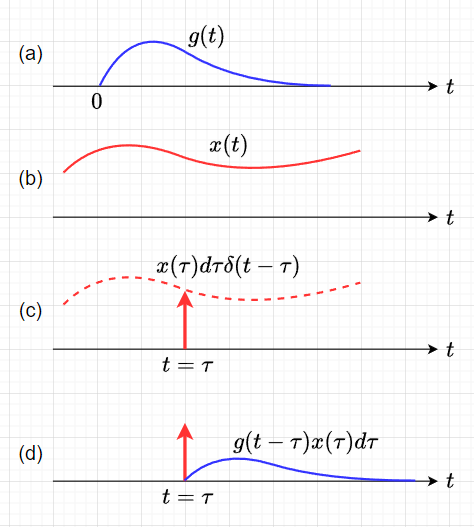
図2(a)のインパルス応答\(g(t)\)を有する線形要素に図2(b)の入力信号\(x(t)\)を印可したときの出力信号\(y(t)\)を考える。入力信号\(x(t)\)から\(t=\tau\)における値を取り出すと図2(c)に示すインパルス\(x(\tau)d\tau \delta(t-\tau)\)となる。このインパルスに対する応答は、図2(d)で示す\(g(t- \tau)x(\tau)d\tau\)となる。従って、入力信号\(x(t)\)に対する出力信号\(y(t)\)は、要素が線形であるから、重ね合わせの理により、$$y(t) = \int_{-\infty}^{\infty} g(t - \tau)x(\tau) d \tau$$となる。
因果システムであれば、\(g(t) = 0 \;\;\;(t < 0)\)なので、$$y(t) = \int_{-\infty}^{t} g(t - \tau)x(\tau) d \tau$$であり、変形すると$$y(t) = \int_{0}^{\infty} g(\tau)x(t-\tau) d \tau$$となる。さらに、入力信号が\(x(t)=0 \;\;\;(t<0)\)であれば、$$y(t) = \int_{0}^{t} g(\tau)x(t-\tau) d \tau$$とできる。
畳み込み積分のラプラス変換
畳み込み積分で表された信号\(y(t)\) $$y(t) = \int_{0}^{t} g(\tau)x(t-\tau) d \tau$$のラプラス変換を考える。$$\mathcal{L}\{y(t)\} = \int_0^{\infty}y(t)e^{-st} dt = \int_0^{\infty} \left[\int_0^{t} g(\tau)x(t - \tau)d \tau \right] e^{-st} dt \\ = \int_0^{\infty} \left[ \int_0^{\infty} g(\tau)x(t - \tau)d \tau \right]e^{-st} dt \\ = \int_0^{\infty} g(\tau) \left[ \int_{\tau}^{\infty} x(t - \tau) e^{-s( t - \tau)} dt \right]e^{-s \tau}d \tau \\ = \int_0^{\infty}g(\tau)e^{-s\tau}d \tau \int_0^{\infty} x(\tau')e^{-s\tau'}d \tau' \cdots\cdots(1)$$すなわち、\(y(t),\;g(t),\;x(t)\)のラプラス変換をそれぞれ\(Y(s),\; G(s),\;X(s)\)とすると、式(1)は、$$Y(s) = G(s)X(s)$$と表せる。以上から、時間領域の畳み込み積分は、ラプラス変換後の複素数領域では積の形となることがわかる。

