14. 電力の測定法
電力は、電流と電圧の積として定義される。電力の測定は、通常、電力計を使用して行われる。電力の測定法に関する基本的な事項は、以下である。
1)電力を測定するためには、適切な電力計を選択する。電力計には、直流または交流の電力を測定するためのものがあり、測定範囲に合った電力計を選ぶことが重要である。
2) 電力計は通常、電流と電圧の両方を同時に測定することができる。電力計を正確に使用するためには、電流計と電圧計を正しい位置に接続する。一般的には、電流計は回路に直列に、電圧計は回路に並列に接続される。
3)電力計は、電圧と電流の積を計算して電力を計測する。電力計は、電流センサと電圧センサからの情報を取得し、それぞれの信号を増幅して乗算することで電力を計算する。
4)近年ではディジタル電力計が一般的である。この電力計は、マイクロプロセッサやディジタル信号処理技術を使用して、高度な機能を提供する。ディジタル電力計は、波形の変動や非正弦波に対する対応が可能であり、通常は電力因数(力率)や周波数なども表示できる。
電力因数:電気エネルギーが効率的に使用されているかを示す指標、有効電力と全体の電力(皮相電力)の比率で求める。
※電力に関しては、電力と電力量を参考にしてください。
電力の定義
電気が単位時間に行なう仕事の量(仕事率)を電力という。負荷抵抗を\(R\)、負荷抵抗に流れる電流を\(I\)、としたとき、電力\(P\)は、$$P = I^2 \cdot R \; [W] ,\;[J/s]$$である。オームの法則より、$$P = V \cdot I \\ P = \frac{V^2}{R}$$と表せる。
オームの法則
\(I=\frac{V}{R}\):抵抗\(R\)に電圧\(V\)を印可したときに流れる電流は\(I\)
(抵抗\(R\)で電圧降下が\(V\)のときの流れる電流は\(I\))
\(V=R\cdot I\):抵抗\(R\)に電流\(I\)が流れるときの印可電圧は\(V\)
(抵抗\(R\)に電流\(I\)を流したときの電圧降下は\(V\))
\(R=\frac{V}{I}\)(電圧\(V\)を印可して電流\(I\)が流れるときの抵抗は\(R\))
(電圧降下が\(V\)で電流\(I\)が流れるときの抵抗は\(R\))
※( )内は工学的な表現
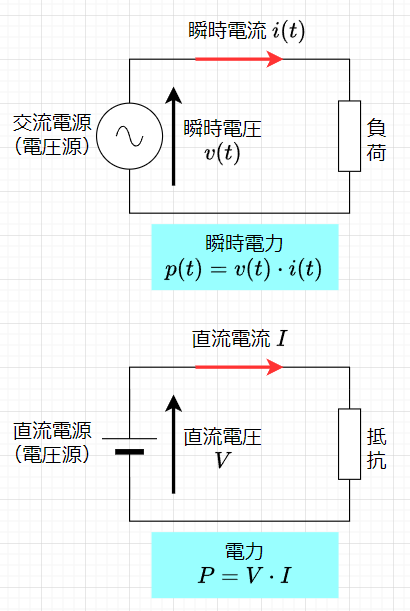
瞬時電力、直流電力
交流電源(交流電圧源)に負荷(抵抗、インダクタ、キャパシタ等)を接続した時の消費電力(瞬時電力)は、$$p(t) = v(t) \cdot i(t)$$と、時間の関数となる。ここで、\(v(t)\)は、瞬時電圧、\(i(t)\)は瞬時電流である。
一方、直流電源(直流電圧源)に負荷(抵抗)を接続した時の消費電量は、$$P = V \cdot I$$となる。ここで、\(V\)は、直流電圧、\(I\)は直流電流である。直流の場合の電力計測は、電圧計、電流計で測定して、その積で求める。もしくは、電流力計形電力計を使用する。
単相交流電力
単相の交流電力を考える。一般に正弦波交流で考えるので、瞬時電圧\(v(t)\)は、$$v(t) = \sqrt{2} V \sin(\omega t + \theta)$$と表せる。ここで、\(\theta\):初期位相角、\(V\):実効値である。瞬時電流\(i(t)\)は、$$i(t) = \sqrt{2} I \sin(\omega t + \theta - \phi)$$と表せる。ここで、\(I\):実効値である。なお、\(\phi\)は負荷によって変わってくる。
従って、瞬時電力\(p(t)\)は、$$p(t) = v(t) \cdot i(t) \\= \sqrt{2}V \sin(\omega t + \theta)\cdot\sqrt{2} I \sin(\omega t + \theta - \phi) \\=2 V \cdot I\times \frac{1}{2} \left\{ \cos \phi - \cos(2\omega t + 2 \theta - \phi)\right\} \\ = V\cdot I \cos \phi - V\cdot I \cos(2\omega t + 2\theta - \phi)$$と表せる。\(V\cdot I \cos(2\omega t + 2\theta - \phi)\)の項は、正弦波振動項なので、その平均値は0となる。従って、平均電力\(P\)は、$$P=\frac{1}{T} \int_0^T p(t) dt = V\cdot I \cos \phi$$となる。\(\cos\phi\)を力率という。図2に示すように、皮相電力\(S\)、有効電力\(P\)、無効電力\(Q\)は、$$S = V \cdot I \;[VA] \\ P = V \cdot I \cos \phi \;[W] \\ Q = V \cdot I \sin \phi \;[var]$$となる。また、$$S = \sqrt{P^2 + Q^2}$$である。\(\cos \phi\)力率は、負荷が消費する電力の割合を示している。
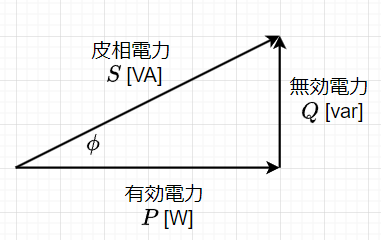
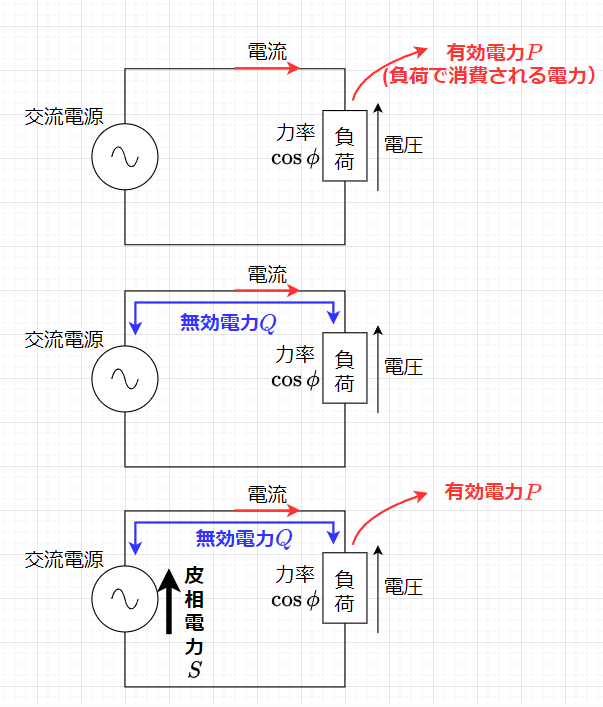
図3に、有効電力、無効電力、皮相電力の関係を示す。有効電力\(P\)は、負荷で消費される電力で、(純)抵抗によって消費され、電気エネルギーが熱エネルギーに変換される。一方、無効電力\(Q\)は、負荷と交流電源の間を往復しているだけの電力で、負荷では電力は消費されない。これは、負荷のインダクタ成分、キャパシタ成分により、電気エネルギーが充電、放電され、交流電源との間で往復することによる。皮相電力\(S\)は、交流電源から送り出される全電力である。
交流電力の負荷の影響
負荷インピーダンス\(\dot{Z}\)は、$$\dot{Z} = R + jX$$で表される。ここで、\(R\)は(純)抵抗、\(X\)はリアクタンスである。コンデンサ(キャパシタ)\(C\)による容量性リアクタンス\(X_C\)は、$$X_C = \frac{1}{\omega C}$$で、このときのインピーダンスは、\( \dot{Z} = R - jX\)と表される。インダクタ(コイル)\(L\)による誘導性リアクタンス\(X_L\)は、$$X_L = \omega L$$で、このときのインピーダンスは、\( \dot{Z} = R + jX\)と表される。
負荷に印可される電圧\(\dot{V}\)を基準に考えると、$$\dot{I} = \frac{\dot{V}}{\dot{Z}} = \frac{\dot{V}}{R + jX}$$なので、電力\(P\)は、$$P = \dot{V} \cdot \dot{I} = \frac{\dot{V}^2}{R + jX} = \frac{R - jX}{\sqrt{R^2 + X^2}}\dot{V}^2$$である。電圧\(\dot{V}\)が基準なので、電力\(P\)の位相は、\(\frac{1}{R + jX}\)で決まり、$$\phi = - \tan^{-1}\left(\frac{X}{R}\right)$$となる。また、力率は、$$\cos \phi = \frac{R}{\sqrt{R^2 + X^2}}$$である。
図4に誘導性負荷に交流電源を接続した場合の電圧と電流の関係を示す。誘導性負荷の場合、電圧(青線)に対して、電流(赤線)の位相が遅れる。従って、この時の無効電力は遅れ無効電力となり、力率は遅れ力率となる。
一方、図5の容量性負荷に交流電源を接続した場合の電圧と電流の関係は、電圧(青線)に対して、電流(赤線)の位相が進む。従って、この時の無効電力は進み無効電力となり、力率は進み力率となる。
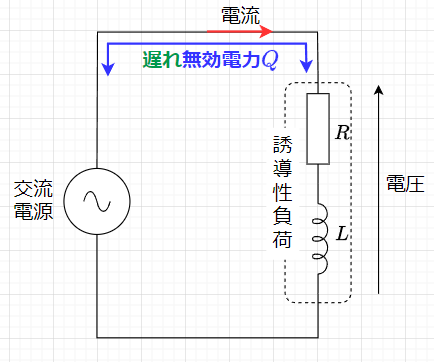
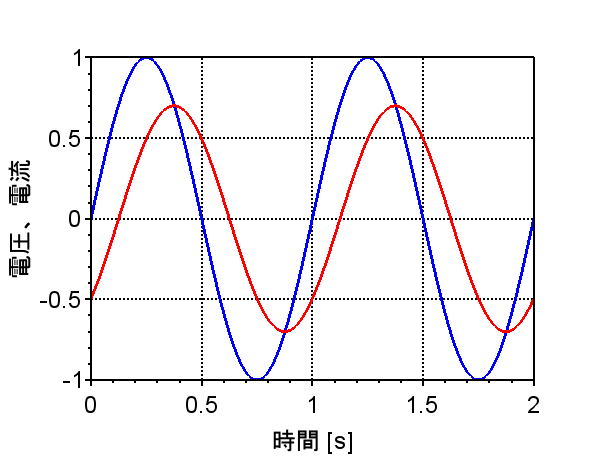
青:電圧、赤:電流
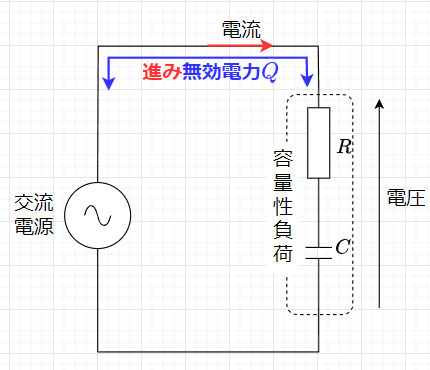
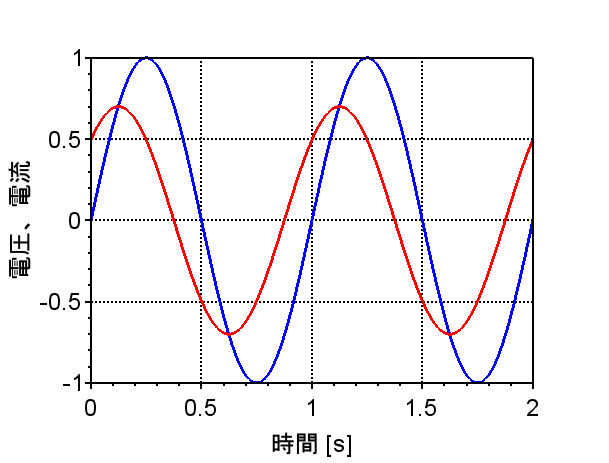
青:電圧、赤:電流
単相電力計
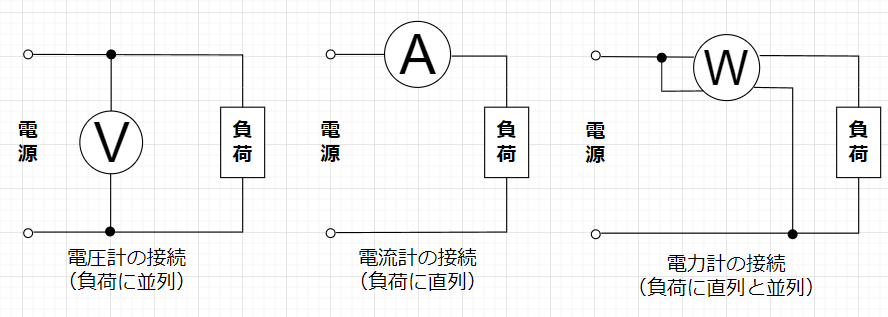
図6に電圧計、電流計、電力計の接続法を示す。電圧計は、負荷に並列に接続する。電流計は、負荷に直列に接続する。また、電力計は、負荷に直列と並列に接続する。
図7に単相電力計の構成を示す。固定コイルは、負荷に直列に接続される電流コイルで、可動コイルは、負荷に並列に接続される電圧コイルである。
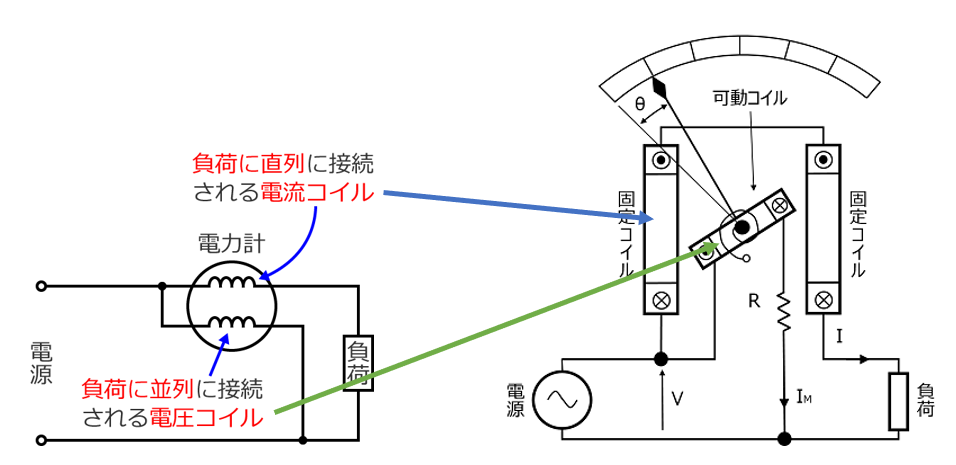
図7の指針形計器の電流力計形電力計の動作原理は、以下である。円筒となっている固定コイルに電流\(I\)が流れると、円筒内部に磁界が形成される。その中に置かれ、軸を中心に回転する可動コイルに電流\(I_M\)が流れると、この可動コイルに駆動トルクが発生し回転することで、指針が動く。駆動トルクは、2つの電流\(I\)、\(I_M\)の瞬時値の積に比例し、平均トルクは電力に比例する。従って、固定コイルに電流を流し、可動コイルに電圧に比例する電流\(I_M = V/R\)を流すことで、指針は電力を指すことになる。
三相電力の計測
※三相交流については、三相交流回路の電圧と電流を参照して欲しい。相電圧、相電流、線間電圧、線電流、Y結線、Δ結線、三相負荷などを確認して、以下を読んでください。
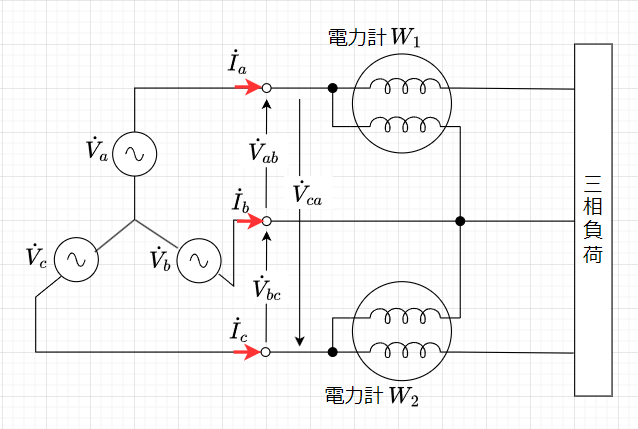
図8が電力計(\(W_1 ,\;\;\; W_2\))2台を使用した三相電力測定の構成図である。
三相電力は各相の電力の和なので、
\(P = \)3 \(\times\)相電圧 \(\times\) 相電流 \(\times\)力率 となる。
有効電力で考えると 、\(\dot{I}_a + \dot{I}_b + \dot{I}_c = 0\)なので、$$P = \dot{V}_a \dot{I}_a + \dot{V}_b \dot{I}_b + \dot{V}_c \dot{I}_c \\ = \dot{V}_a \dot{I}_a - \dot{V}_b( \dot{I}_a + \dot{I}_c ) + \dot{V}_c \dot{I}_c \\=( \dot{V}_a - \dot{V}_b ) \dot{I}_a + ( \dot{V}_c - \dot{V}_b )\dot{I}_c \\= \dot{V}_{ab} \dot{I}_a + \dot{V}_{cb} \dot{I}_c$$となる。
従って、2つの線間電圧( \(\dot{V}_{ab} , \;\; \dot{V}_{cb} = - \dot{V}_{bc}\) )と2つの線電流( \(\dot{I}_a ,\;\; \dot{I}_c\))で電力が計測できることになる。