14-1. バタワースフィルタ
バターワースフィルタは、通過帯域における周波数特性が最大限平坦になるように設計されたアナログフィルタの一種である。リップルと呼ばれる通過帯域におけるゲインの変動がなく、減衰特性は周波数の平方根に比例する。
バタワースフィルタの特徴は、
・通過帯域が平坦: 通過帯域における周波数特性が平坦なので、信号の歪みを最小限に抑えることができる。
・減衰特性: 減衰特性は、周波数の平方根に比例する。
・設計が容易: 数学的な計算が比較的簡単であるため他のフィルタに比べて設計が容易。
バタワースフィルタは、次数が高くなるほど、通過帯域の平坦性が高くなり、減衰特性の傾きが急になる。
・1次:最もシンプルなバターワースフィルタで、通過帯域の平坦性は低く、減衰特性の傾きも緩やか。
・2次:多くの用途で用いられる一般的なバターワースフィルタで、通過帯域の平坦性と減衰特性のバランスが良い。
・3次以上:高い平坦性と急峻な減衰特性が必要な場合に用いられる。
バターワースフィルタは、 動作が安定しており、発振などの問題が発生しにくいが、遮断周波数付近の減衰特性は緩やかである。
※以下の説明の周波数伝達関数については、18. システムの周波数応答を参考にして下さい。
CRバタワースLPF
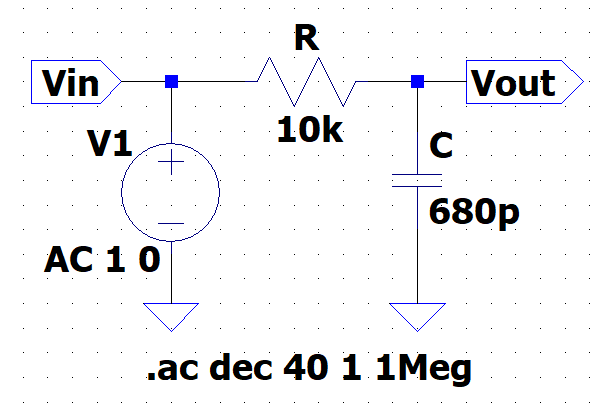
図1にコンデンサ\(C\)と抵抗\(R\)で構成するCRバタワースLPFを示す。\(R,\;C\)に流れる電流を\(i(j\omega)\)とすると、$$V_{in}(j \omega) =\left( R + \frac{1}{j \omega C} \right)i(j \omega)\\V_{out}(j \omega) = \frac{1}{j \omega C} i(j \omega)$$となる。
LTspice
従って、周波数伝達関数\(G(j \omega)\)は、$$G( j \omega) =\frac{V_{out}(j \omega)}{V_{in}(j \omega)} = \frac{1}{1 + j \omega CR}$$である。ここで、\(\frac{1}{CR} = \omega_0\)とおくと、$$G(j \omega) = \frac{1}{1 + j \left(\frac{\omega}{\omega_0}\right)}$$と書ける。\(\frac{\omega}{\omega_0}\)を正規化角周波数(正規化周波数)という。振幅特性\(|G(j\omega)|\)は、$$|G(j \omega)| = \frac{1}{\sqrt{ 1 + \left(\frac{\omega}{\omega_0}\right)^2}}$$また、位相特性\(\angle{G(j\omega}\)は、$$\angle{G(j \omega)} = -\tan^{-1} \left(\frac{\omega}{\omega_0}\right)$$である。\(\frac{\omega}{\omega_0} = 1\)のとき、振幅特性は、\(\frac{1}{\sqrt{2}}\)、位相特性は、\(-45\)度となる。\(\frac{\omega}{\omega_0} = 1\)となる角周波数\(\omega\)は、\(\omega_0\)なので、周波数は\(f_c=\frac{\omega_0}{2 \pi}\)であり、この\(f_c\)を遮断周波数(カットオフ周波数)という。
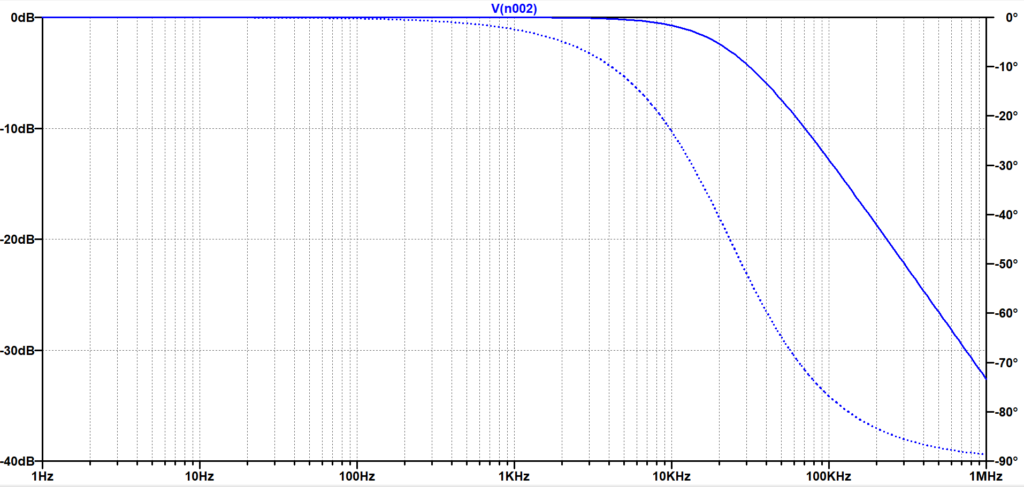
図2は、LTspiceのAC解析により求めた、図1の回路の周波数特性である。\(f_c\)以上より周波数が十分に低い低周波数領域では、振幅は\(0 \;dB\)、位相は\(0\)度で、\(f_c =\frac{1}{2 \pi CR}\approx 23.4\;kHz\)において、\(-3\; dB(=\frac{1}{\sqrt{2}})\)となり、その時、位相は、\(-45\) 度となる。また、\(f_c\)以上の高周波数領域では、振幅特性は\(-20dB/dec\)となり、位相は、\(-90\) 度まで遅れる。
CRバタワースHPF
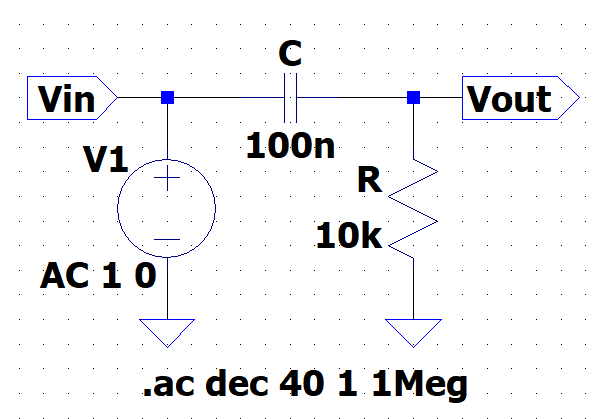
図3にコンデンサ\(C\)と抵抗\(R\)で構成するCRバタワースHPFを示す。\(R,\;C\)に流れる電流を\(i(j\omega)\)とすると、$$V_{in}(j \omega) =\left( \frac{1}{j \omega C} + R\right)i(j \omega)\\V_{out}(j \omega) = R i(j \omega)$$となる。
LTspice
従って、周波数伝達関数\(G(j \omega)\)は、$$G( j \omega) =\frac{V_{out}(j \omega)}{V_{in}(j \omega)} = \frac{R}{R + \frac{1}{j \omega C} }= \frac {j \omega CR}{1 + j \omega CR}$$である。ここで、\(\frac{1}{CR} = \omega_0\)とおくと、$$G(j \omega) = \frac{j \left(\frac{\omega}{\omega_0}\right)}{1 + j \left(\frac{\omega}{\omega_0}\right)}$$と書ける。\(\frac{\omega}{\omega_0}\)を正規化角周波数(正規化周波数)という。振幅特性\(|G(j\omega)|\)は、$$|G(j \omega)| = \frac{\frac{\omega}{\omega_0}}{\sqrt{ 1 + \left(\frac{\omega}{\omega_0}\right)^2}}$$また、位相特性\(\angle{G(j\omega}\)は、$$\angle{G(j \omega)} =\frac{\pi}{2} -\tan^{-1} \left(\frac{\omega}{\omega_0}\right)$$である。\(\frac{\omega}{\omega_0} = 1\)のとき、振幅特性は、\(\frac{1}{\sqrt{2}}\)、位相特性は、\(-45\)度となる。\(\frac{\omega}{\omega_0} = 1\)となる角周波数\(\omega\)は、\(\omega_0\)なので、周波数は\(f_c=\frac{\omega_0}{2 \pi}\)であり、この\(f_c\)を遮断周波数(カットオフ周波数)という。
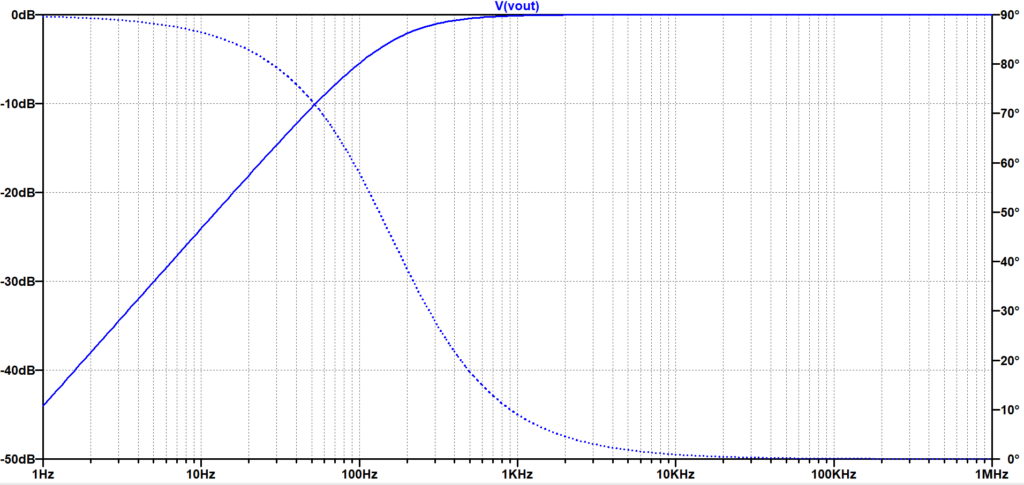
図4は、LTspiceのAC解析により求めた、図3の回路の周波数特性である。(f_c\)以上より周波数が十分に高い高周波数領域では、振幅は\(0 \;dB\)、位相は\(0\)度で、i\(f_c =\frac{1}{2 \pi CR}\approx 159\;Hz\)において、\(-3\; dB(=\frac{1}{\sqrt{2}})\)となり、その時、位相は、\(+45\) 度となる。また、\(f_c\)以下の低周波数領域では、振幅特性は\(+20dB/dec\)となり、位相は、\(+90\) 度まで進む。
CRバタワースBPF
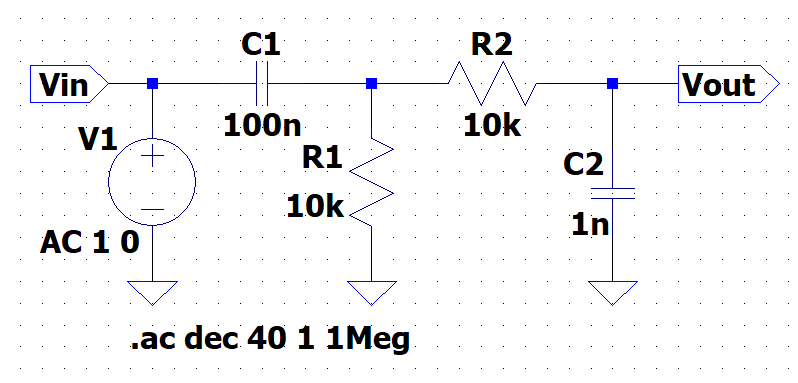
図5にコンデンサ\(C\)と抵抗\(R\)で構成するCRバタワースBPFを示す。図5のようにLPFとHPFをカスケード接続することで実現できる。BPFでは、遮断周波数は\(f_{c1}\)と\(f_{c2}\)の2ヶ所となる。
LTspice
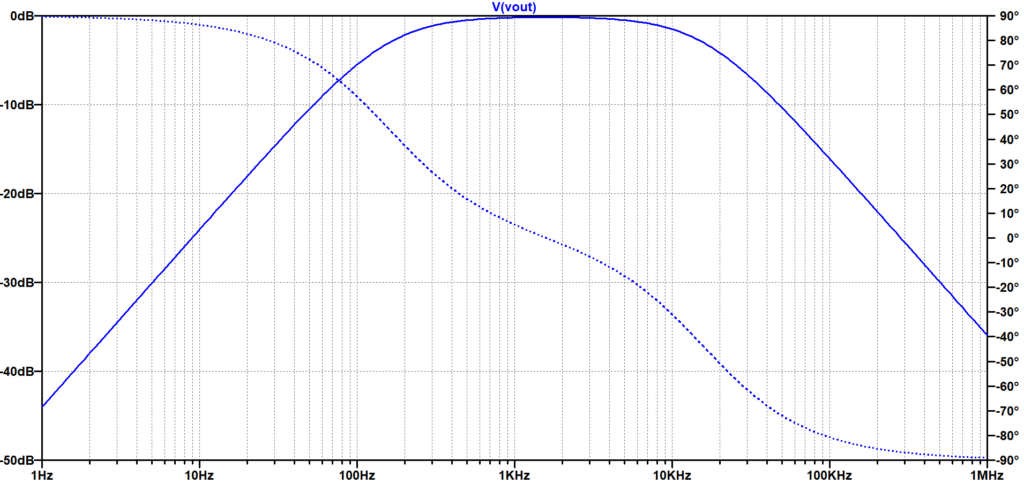
図6は、LTspiceのAC解析により求めた、図5の回路の周波数特性である。\(f_{c1}\)以下の低周波数域ではHPF特性、\(f_{c2}\)以上の高周波数域ではLPF特性となっており、\(f_{c1}\)と\(f_{c2}\)の周波数帯域が通過帯域となっている。\(f_{c1} \approx 159\;Hz\)で、\(f_{c2} \approx 15.9\;kHz\)である。低周波数域では、振幅特性は\(20\;dB/dec\)、位相特性は\(90\)度の位相進みに近くなり、高周波数域では、振幅特性は\(-20\;dB/dec\)、位相特性は\(-90\)度の位相遅れに近くなる。通過帯域では、振幅特性は約\(0 \; dB\)、位相特性は、約\(0\)度となる。
LRバタワースフィルタ
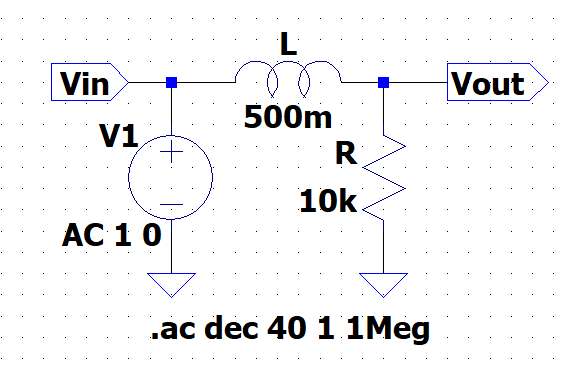
図7にインダクタ\(L\)と抵抗\(R\)で構成するLRバタワースLPFを示す。\(R,\;L\)に流れる電流を\(i(j\omega)\)とすると、$$V_{in}(j \omega) =\left( R + j \omega L \right)i(j \omega)\\V_{out}(j \omega) = R i (j\omega)$$となる。
LTspice
従って、周波数伝達関数\(G(j \omega)\)は、$$G( j \omega) =\frac{V_{out}(j \omega)}{V_{in}(j \omega)} = \frac{R}{R + j \omega L} = \frac{1}{1 + j \left(\frac{\omega L}{R}\right)}$$である。ここで、\(\frac{R}{L} = \omega_0\)とおくと、$$G(j \omega) = \frac{1}{1 + j \left(\frac{\omega}{\omega_0}\right)}$$と書ける。\(\frac{\omega}{\omega_0}\)を正規化角周波数(正規化周波数)という。振幅特性\(|G(j\omega)|\)は、$$|G(j \omega)| = \frac{1}{\sqrt{ 1 + \left(\frac{\omega}{\omega_0}\right)^2}}$$また、位相特性\(\angle{G(j\omega}\)は、$$\angle{G(j \omega)} = -\tan^{-1} \left(\frac{\omega}{\omega_0}\right)$$である。\(\frac{\omega}{\omega_0} = 1\)のとき、振幅特性は、\(\frac{1}{\sqrt{2}}\)、位相特性は、\(-45\)度となる。\(\frac{\omega}{\omega_0} = 1\)となる角周波数\(\omega\)は、\(\omega_0\)なので、周波数は\(f_c=\frac{\omega_0}{2 \pi}\)であり、この\(f_c\)を遮断周波数(カットオフ周波数)という。 この伝達関数は、CRバタワースLPFの伝達関数と同じ形であり、同様な周波数特性を持つことが分かる。
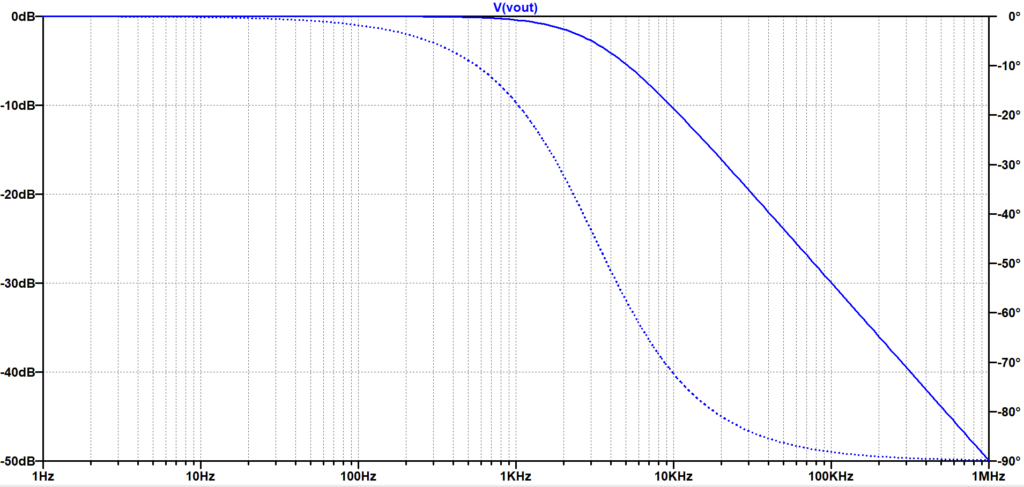
図8は、LTspiceのAC解析により求めた、図7の回路の周波数特性である。\(f_c\)以上より周波数が十分に低い低周波数領域では、振幅は\(0 \;dB\)、位相は\(0\)度で、\(f_c =\frac{R}{2 \pi L}\approx 3.18\;kHz\)において、\(-3\; dB(=\frac{1}{\sqrt{2}})\)となり、その時、位相は、\(-45\) 度となる。また、\(f_c\)以上の高周波数領域では、振幅特性は\(-20dB/dec\)となり、位相は、\(-90\) 度まで遅れる。
また、これと同様にして、LRによるバタワースHPF、バタワースBPFを構成することもできる。
2次バタワースフィルタ
前述のCRやLRの1組で構成される1段のフィルタ回路を1次フィルタと称し、2段に組み合わせたフィルタを2次フィルタと称する。バタワースLPFの場合、次数が増えると高周波数域での振幅の減衰特性が急になり、1次の場合、\(-20 \; dB/dec\)の減衰率が、2次の場合、\(-40\;dB/dec\)となる。
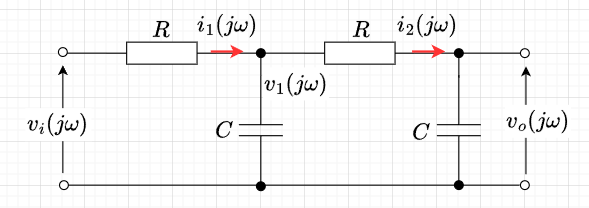
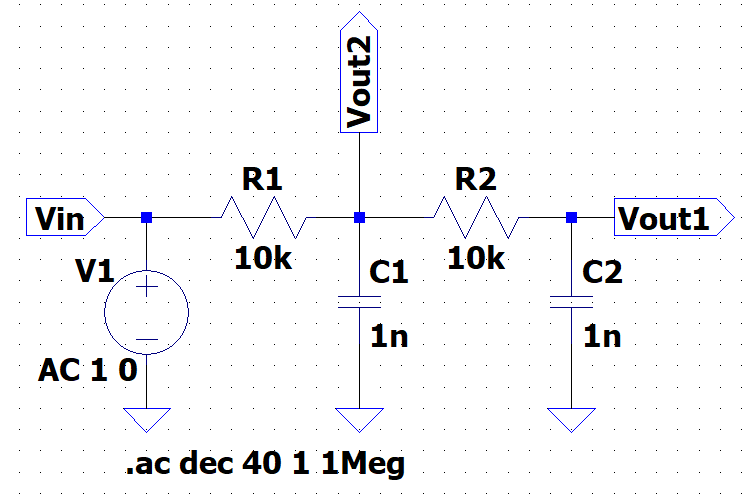
LTspice
図9より、周波数伝達関数\(G( j \omega)\)を求める。$$v_i - v_1 = R i_1 \;\;\;\;\;\; v_1 = \frac{1}{sC}(i_1 - i_2) \\ v_1 - v_o = R i_2 \;\;\;\;\;\; v_o = \frac{1}{sC} i_2$$これより、$$\frac{v_o}{v_i} = \frac{1}{(sCR)^2 + 3sCR + 1}$$ さらに、\(s \rightarrow j \omega\)とすると、$$G(j \omega) = \frac{v_o(j \omega)}{v_i(j \omega)} = \frac{1}{1 - (\omega CR)^2 +j 3\omega CR}$$と周波数伝達関数が求まる。周波数伝達関数から分かるように、高周波数領域では、\(\frac{1}{ \omega^2}\)の特性となる。つまり、振幅特性は\(-40\;dB/dec\)で、位相特性は\(-180\)度までの位相遅れとなる。
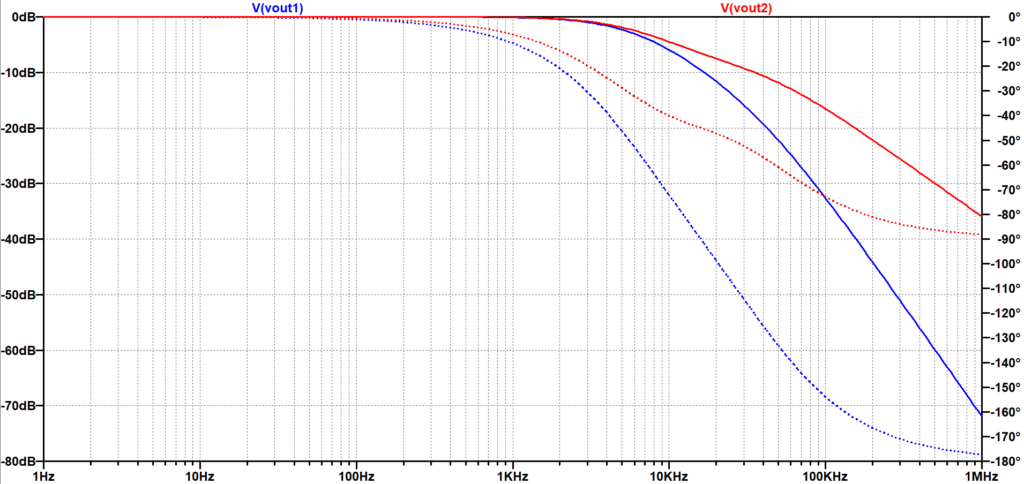
図10が2次バタワースLPFの例である。1段目、2段目のC、Rの値を同じとしてあるため、1段目、2段目の遮断周波数は変わらない。図の赤線が1段目までの(\(V_{out}2\))の振幅特性と位相特性、図の青線が2段目までの(\V_{out}1\))の振幅特性と位相特性である。1段目までは、遮断周波数以上の高周波数領域で振幅特性は、\(-20\;dB/dec\)であり、位相特性は、\(-90\)度まで遅れる。2段目まででは、遮断周波数以上の高周波数領域で振幅特性は、\(-40\;dB/dec\)で急峻な減衰特性となる。一方、位相特性は、\(-180\)度まで大きく変化し位相が遅れる。


“14-1. バタワースフィルタ” に対して2件のコメントがあります。
コメントは受け付けていません。