14-3. チェビシェフフィルタ
チェビシェフフィルタは、フィルタの一種で、バターワースフィルタに比べてロールオフ(フィルタの帯域の端における通過特性の変化の急峻さ)が急勾配で、通過帯域にリップルがある場合(第一種)と阻止帯域にリップルがある場合(第二種)がある。
・第一種チェビシェフフィルタ:ローパスフィルタの特性は、リップル係数とチェビシェフ多項式によって決まる。通過帯域ではリップルがあるため、高調波を含む信号には適していない。ただし、リップルは通過帯域における信号の反射を調整し、電圧定在波比(VSWR)を適切な範囲に保つ役割を果たす。
・第二種チェビシェフフィルタ:通過帯域にはリップルがないため、高調波を含む信号にも適している。ただし、遮断特性を急峻にするためにはより多くの部品が必要である。
チェビシェフフィルタは、理想的なフィルタ特性と実装との間で誤差を最小化する特徴を持つ。
チェビシェフ多項式
チェビシェフ多項式は、三角関数の性質と多項式の関連性の研究から発見されたもので、数学、物理学、工学、統計学などのさまざまな分野で応用されている。
第一種チェビシェフ多項式は、式(1)で定義される。$$T_n(x) = \cos(nt), \;\;\;\; x=\cos t \;\; \cdots (1)$$ $$\cos 0t = 1, \;\;\;\;\cos 1t = \cos t, \\ \cos 2t = 2 \cos^2 t -1, \\ \cos 3t = 4 \cos^3 t - 3 \cos t, \\ \cdots \cdots$$ よって、$$T_0(x) =1,\;\;\;\; T_1(x) = x , \\ T_2(x) = 2 x^2 -1, \\T_3(x) = 4 x^3 -3 x, \\T_4(x) = 8 x^4 - 8 x^2 +1, \\ \cdots \cdots$$となる。従って、これは三項間漸化式で表せ、$$T_{n+1}(x) = 2x T_n(x) - T_{n-1}(x) ,\\ (n = 1,2,3,\cdots)$$ となる。図1に\(n=0,1,2,3,4\)までの第1種チェビシェフ多項式のグラフを示す。
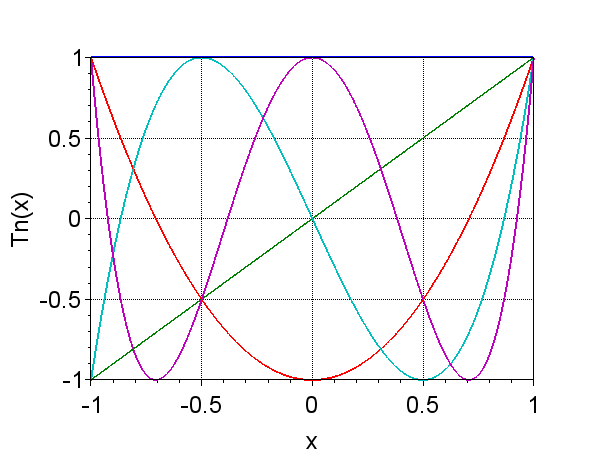
(\(n=0,1,2,3,4\))
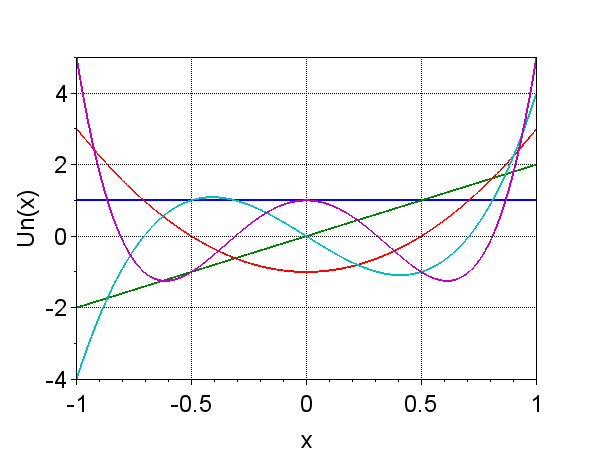
(\(n=0,1,2,3,4\))
第二種チェビシェフ多項式は、式(2)で定義される。$$U_{n-1}(\cos t) = \frac{\sin nt}{\sin t} \;\; \cdots (2)$$ $$U_0(x) = 1, \;\;\;\; U_1(x) = 2x, \;\;\;\; U_2(x) = 4x^2 -1, \\ U_3(x) = 8x^3 - 4x, \;\;\;\; U_4(x) =16 x^4 - 12 x^2 +1, \cdots \cdots$$となり、$$n U_{n-1}(t) = T_n^{'}(t)$$の関係なので、$$U_{n+1}(x) = 2x U_n(x) - U_{n-1}(x), \\(n = 1,2,3,\cdots)$$の三項間漸化式で表せる。図2に\(n=0,1,2,3,4\)までの第2種チェビシェフ多項式のグラフを示す。
以上の第一種、第二種チェビシェフ多項式から導出されたのが、チェビシェフフィルタの特性となる。
チェビシェフフィルタの特性
第一種チェビシェフフィルタ
第一種チェビシェフ多項式から導かれる\(n\)次チェビシェフLPFの利得特性は、式(3)となる。$$|G_n(\omega)| = \frac{1}{\sqrt{ 1 + \epsilon ^2 T_n^2\left(\frac{\omega}{\omega_0}\right)}}\;\;\cdots (3)$$ ここで、\(\epsilon\)はリップル係数、\(\omega_0\)は遮断周波数、\(T_n( )\)が\(n\)次のチェビシェフ多項式である。
通過帯域は等リップル性を示し、そのリップルはリップル係数\(\epsilon\)で決定される。通過帯域ではチェビシェフ多項式は \(-1\) から \(1\) の範囲で変化し、チェビシェフ多項式の2乗は 0 から 1 の範囲で変化するので、フィルタの利得は最大 \(|G_n(\omega)|=1\) から最小\(|G(\omega)| = \frac{1}{\sqrt{1 + \epsilon^2}}\)間で変化する。遮断周波数\(\omega_0\)での利得は、第一種チェビシェフ多項式から、\(\frac{1}{\sqrt{1 + \epsilon^2}}\)となる。\(\left(\frac{\omega}{\omega_0}\right) > 1\)のとき、つまり\(T_n(x)\)で\( x>1\)のとき、\(T_n( )\)は急激に大きくなるので、式(3)より、チェビシェフフィルタの利得は急峻に低下し、阻止帯域となる。
| \(n\) | \(R_s\) | \(C_1\) | \(L_2\) | \(C_3\) | \(L_4\) | \(C_5\) |
| 3 | 1.000 | 1.864 | 1.280 | 1.864 | ||
| 5 | 1.000 | 1.807 | 1.302 | 2.691 | 1.302 | 1.807 |
入力インピーダンス\(50\; \Omega\)、遮断周波数\(f_c = 100 \;kHz\)、\(0.5 \;dB\)リップルのチェビシェフLPFを表1の係数表を使い設計する。
\(\omega_c = 2 \pi f_c = 6.2832\times 10^5\; rad/s \)
・3次チェビシェフLPFの設計値
$$R_s = 1.000\times 50 \\ C_1 = \frac{1.864}{\omega_c \times 50} = 59.33\; nF \\L_2 = \frac{1.280 \times 50}{\omega_c} = 0.1019\; mH \\C_3 = C_1$$図3に回路図を示す。また、 図4に周波数特性を示す。
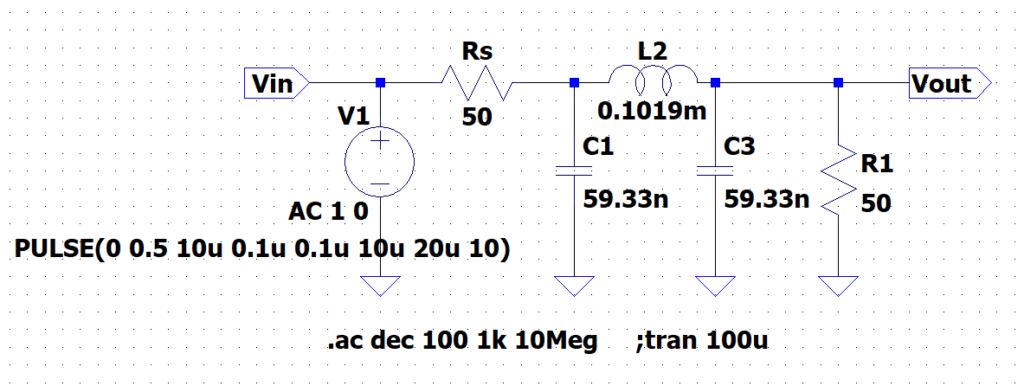
3次チェビシェフLPF
LTspice
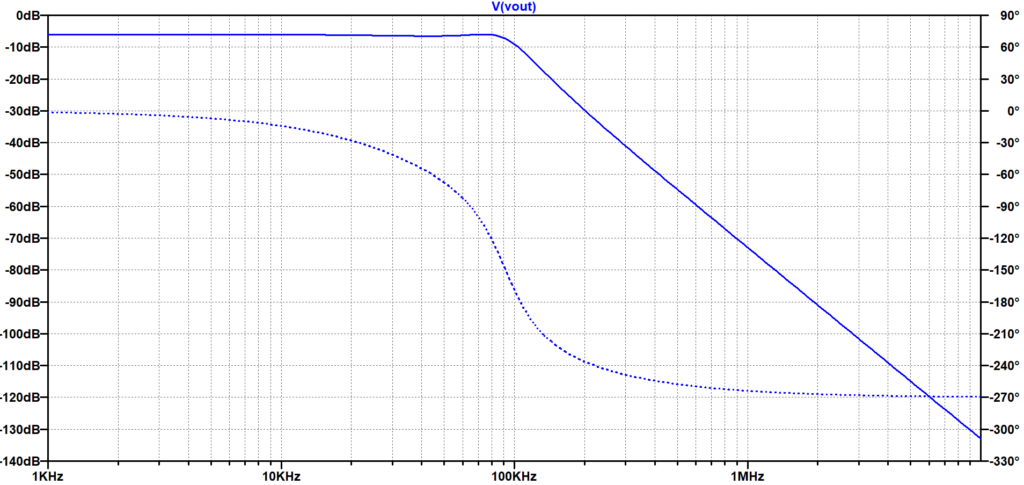
・5次チェビシェフLPFの設計値
$$R_s = 1.000\times 50 \\ C_1 = \frac{1.807}{\omega_c \times 50} = 57.52 \; nF \\L_2 = \frac{1.302 \times 50}{\omega_c} = 0.1036\; mH \\C_3 = \frac{2.691}{\omega_c \times 50} = 85.66\;nF \\L4 = L2 ,\;\;\; C5 = C1$$
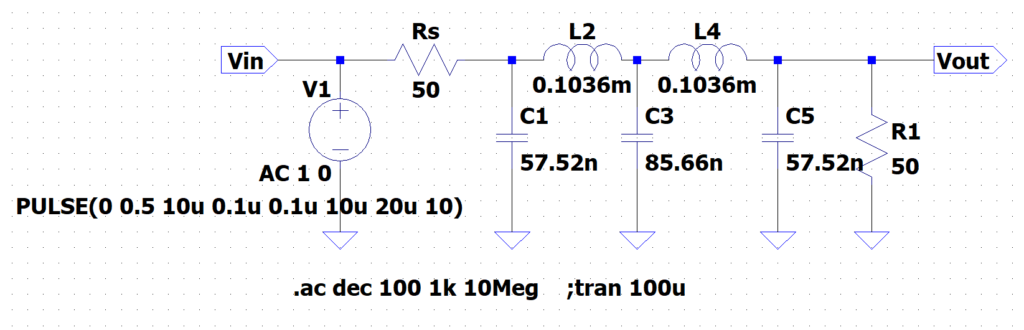
5次チェビシェフLPF
LTspice
図5に回路図を示す。また、 図6に周波数特性を示す。図7は、\(100 \; kHz\)近傍の特性を拡大した特性図である。通過帯域において、\(0.5 dB\)のリップル(周波数に対する振幅の変動)があることが良く分かる。
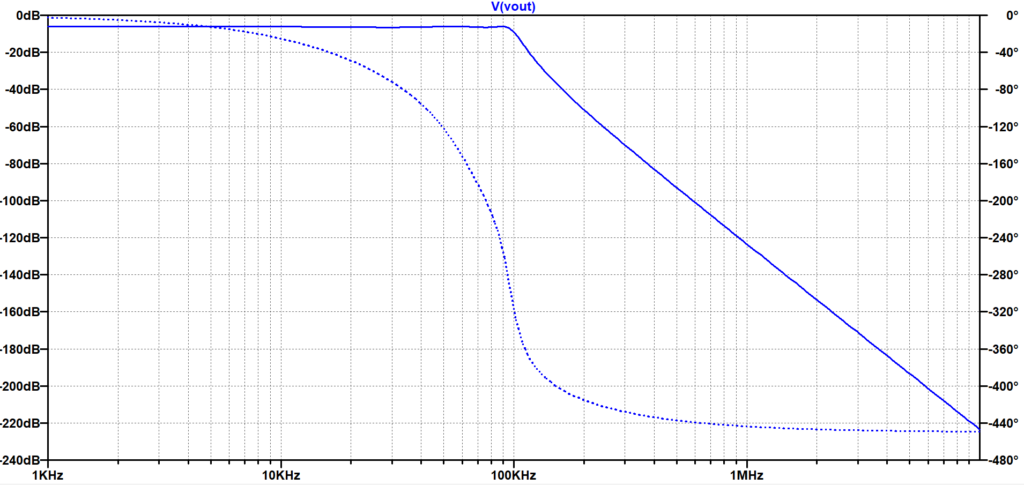
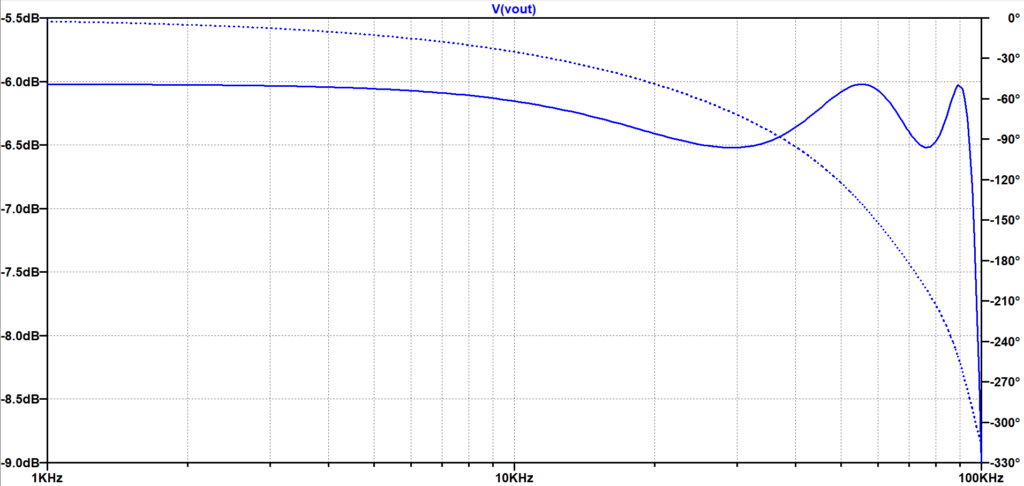
\(100 \;kHz\)近傍での特性


“14-3. チェビシェフフィルタ” に対して1件のコメントがあります。
コメントは受け付けていません。