21. システムの応答(演習)
制御対象を入力\(m\)、出力\(l\)の\(n\)次元の線形定係数システムとする。$$\dot{x}(t) = A x(t) + B u(t) \;\cdots \cdots (1) \\ y(t) = C x(t)\; \cdots\cdots (2)$$ここで、 \(x(t) , \;\;\; u(t), \;\;\; y(t) \)は、それぞれ\(n,\;m,\;l\)次元のベクトル、また、\(A \; (n \times n),\;\;\; B \;(n \times m) ,\;\;\; C \; (l \times n)\)は行列である。式(1)の解は、初期値を\(x_0\)とすると、$$x(t) = e^{A t}x_0 + \int_0^t e^{A(t - \tau)} B u(\tau) d\tau \;\cdots\cdots (3)$$となる。出力の時間応答y(t)は、式(3)を式(2)に代入すれば求まる。
行列指数関数\(e^{At}\)は、$$e^{At} = I + At + \frac{1}{2!}A^2 t^2 + \cdots + \frac{1}{k!}A^k t^k + \cdots$$であり、これを状態遷移行列と呼ぶ。この微分は、$$\frac{d}{dt} e^{At} = A e^{At} =e^{At} A$$である。積分は、$$A \int_0^t e^{A \tau} d \tau = e^{At} - I$$なので、\(A\)が正則行列であれば、$$\int_0^t e^{A \tau} d \tau= A^{-1}(e^{At} - I) = (e^{At} -I)A^{-1}$$である。また、$$e^0 = I ,\;\;\;\; e^{At} e^{A\tau} = e^{A(t + \tau)} , \;\;\;\; (e^{At})^{-1} = e^{-At}$$となる。さらに、ラプラス変換を使うと、$$\mathcal{L}^{-1} \left[ (s I - A)^{-1} \right] = e^{At}$$と表せる。
※詳細は、5. 線形時不変システムの応答、6. システムの安定性を参照願います。
状態遷移行列の計算
\(A = \begin{bmatrix} 2 & -4 \\ 7 & -9 \end{bmatrix}\)の状態遷移行列\(e^{At}\)を求める。
$$(sI - A)^{-1} = \begin{bmatrix} s -2 & 4 \\ -7 & s+ 9 \end{bmatrix}^{-1} \\ = \frac{1}{(s +2)(s + 5)}\begin{bmatrix} s+9 & -4 \\7 & s-2 \end{bmatrix} \\= \begin{bmatrix} \frac{7/3}{s+2} + \frac{-4/3}{s+5} & \frac{-4/3}{s+2} + \frac{4/3}{s+5} \\ \frac{7/3}{s+2} + \frac{-7/3}{s+5} & \frac{-4/3}{s+2} + \frac{7/3}{s+5} \end{bmatrix}$$となり、この逆ラプラス変換により\(e^{At}\)が求まるので、$$e^{At} = \mathcal{L}^{-1} \left[ (s I - A)^{-1} \right] \\ = \begin{bmatrix} \frac{7}{3} e^{-2t} - \frac{4}{3}e^{-5t} & - \frac{4}{3} e^{-2t} + \frac{4}{3} e^{-5t} \\ \frac{7}{3} e^{-2t} - \frac{7}{3} e^{-5t} & -\frac{4}{3} e^{-2t} + \frac{7}{3} e^{-5t} \end{bmatrix}\;\;\cdots(4)$$となる。
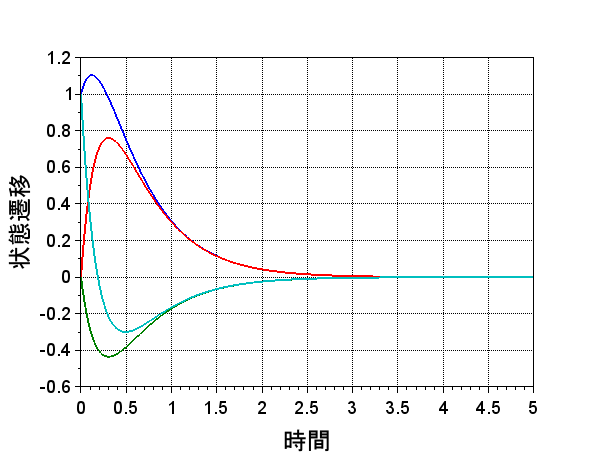
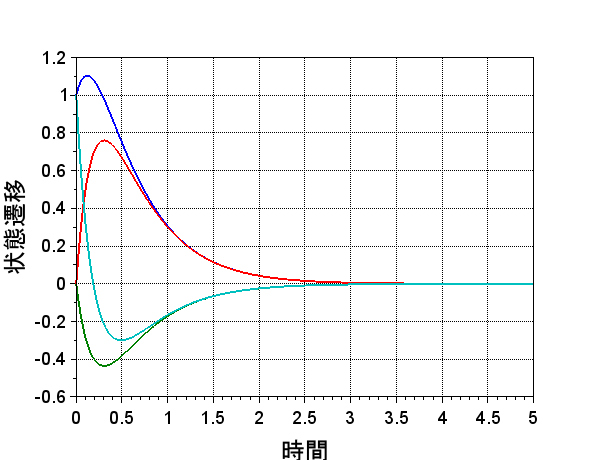
Scilabによる計算結果を図1、図2に示す。図1は、Scilabに実装されている行列指数関数(expm)を使用した状態遷移の計算例で、図2は、式(4)を使用した状態遷移の計算例である。同じ結果が得られることが分かる。システム行列\(A\)のサイズが大きい場合等では、式(4)のような一般解を求めるのが困難になることもある。数値計算として、行列指数関数(expm)を使用して解の振る舞いを求めることは、システムを理解する上で有用である。
Scilabによる状態遷移行列の計算
//状態遷移行列の計算
clear; clf;
MAX_STEP = 500;//ステップ数
dt = 0.01;//刻み時間
A = [2 -4; 7 -9];//システム行列
scf(0);
for i = 1:MAX_STEP
t = (i - 1)*dt;
x = expm(A*t);//行列指数関数
x1(i) = x(1,1);
x2(i) = x(1,2);
x3(i) = x(2,1);
x4(i) = x(2,2);
end;
t = 1:MAX_STEP;
t = (t - 1)*dt;
plot(t,[x1 x2 x3 x4]);
//式(4)による計算
scf(1);
x11 = (7/3)*exp(-2*t) - (4/3)*exp(-5*t);
x12 = (-4/3)*exp(-2*t) + (4/3)*exp(-5*t);
x21 = (7/3)*exp(-2*t) - (7/3)*exp(-5*t);
x22 = (-4/3)*exp(-2*t) + (7/3)*exp(-5*t);
plot(t, [x11' x12' x21' x22']);
線形システムの時間応答
制御対象を$$\dot{x}(t) = \begin{bmatrix} 2 & -4 \\ 7 & -9 \end{bmatrix} x(t) + \begin{bmatrix} 0 \\1 \end{bmatrix}u(t)$$として、初期状態量\(x_0 = \begin{bmatrix} 1 \\ 0 \end{bmatrix}\)また、入力が\(u(t)=1 ,\;t \ge 0\)のときの時間応答を求める。
式(3)より、$$x(t) = e^{At}\begin{bmatrix} 1 \\ 0 \end{bmatrix} + \int_0^t e^{A(t - \tau) } \begin{bmatrix} 0 \\1 \end{bmatrix} d \tau$$ 状態遷移行列は、式(4)なので、$$x(t) = \begin{bmatrix} \frac{7}{3} e^{-2t} - \frac{4}{3}e^{-5t} \\ \frac{7}{3} e^{-2t} - \frac{7}{3} e^{-5t} \end{bmatrix} + \int_0^t \begin{bmatrix} - \frac{4}{3} e^{-2t} + \frac{4}{3} e^{-5t} \\ -\frac{4}{3} e^{-2t} + \frac{7}{3} e^{-5t} \end{bmatrix} d\tau \\ = \begin{bmatrix} \frac{7}{3} e^{-2t} - \frac{4}{3}e^{-5t} \\ \frac{7}{3} e^{-2t} - \frac{7}{3} e^{-5t} \end{bmatrix} + \begin{bmatrix} -\frac{2}{5} + \frac{2}{3} e^{-2t} - \frac{4}{15} e^{-5t} \\ -\frac{1}{5} + \frac{2}{3}e^{-2t} - \frac{7}{15}e^{-5t}\end{bmatrix} \\=\begin{bmatrix} -\frac{2}{5} + 3e^{-2t} - \frac{8}{5}e^{-5t} \\ -\frac{1}{5} + 3e^{-2t} - \frac{14}{5}e^{-5t} \end{bmatrix}\; \cdots\cdots(5)$$となる。
Scilabによるシステムの時間応答
//線形システムの時間応答
clear; clf;
//システムの状態方程式
A=[2 -4 ; 7 -9];
B=[0; 1]; C=[1 0 ; 0 1];
sysP=syslin('c',A,B,C);
x0 = [1; 0];
t=0:0.01:5;
deff('u=timefun(t)', 'u=1');
y=csim(timefun, t, sysP, x0);
scf(0); plot(t',y');
//式(5)による計算
y1 = -2/5 + 3*exp(-2*t) - 8/5*exp(-5*t);
y2 = -1/5 + 3*exp(-2*t) - 14/5*exp(-5*t);
scf(1);plot(t',[y1' y2'])
※Cは状態変数\(x1, x2\)を観測できるように設定している。
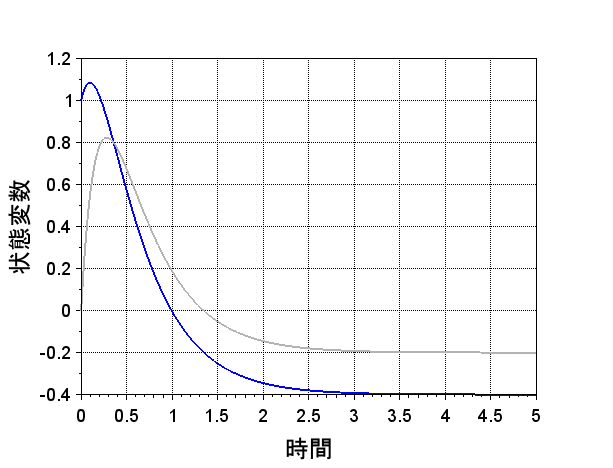
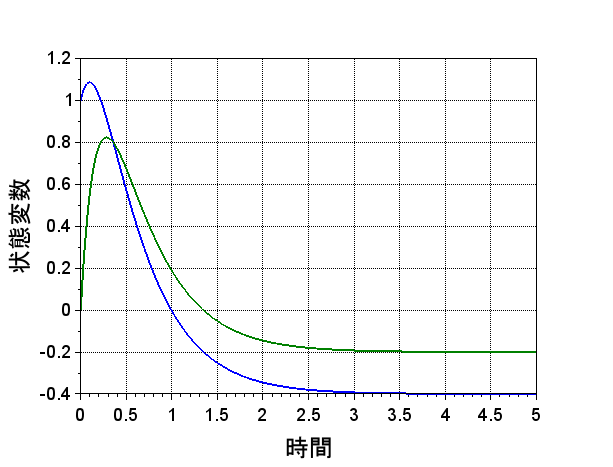
図3にScilabのcsim関数を使用して時間応答を数値計算した場合を示す。システム行列\(A\)、入力行列\(B\)などを設定して容易にシステムの時間応答を計算できる。図4は、式(5)によるシステムの時間応答の計算である。同じ結果が得られることが分かる。システム行列(A)のサイズが大きい場合等では、式(5)のような一般解を求めるのは煩雑である。数値計算により、システムの時間応答を求めることはシステムを直観的に理解する上で有用である。
固有値と応答の関係
\(A \;(n \times n)\)を正方行列とする。このとき、$$| s I - A|=0$$とする\(s\)を\(A\)の固有値という。固有値を\(\lambda_i\)と書く。\(A\)の固有値\(\lambda_i\)に対して、$$A v_i = \lambda_i v_i , \;\;\; i=1,2,\cdots,n$$を満たす\(n\)次元ベクトル\(v_i\)を固有ベクトルという。
固有値\(\lambda_i\)が全て相異なるとした場合(実際のシステムで固有値が完全に重複することは少ないので妥当な仮定と思う)、固有ベクトル\(v_i\)は線形独立となる。これを横に並べた正方行列$$T = [ v_1, \; v_2,\;\cdots ,v_n]$$は正則となる。この行列を使い、\(\dot{x}(t) = A x(t)\)のシステムを\(x(t) = T z(t)\)のように座標変換する。このシステムの解\(x(t)\)は、$$x(t) = e^{At} x(0) = T \begin{bmatrix} e^{\lambda_1 t} & & & &\\ & e^{\lambda_2 t} & & \\ & & \ddots & &\\ & & & e^{\lambda_n t} \end{bmatrix} T^{-1}x(0) \\= \begin{bmatrix} v_1 & v_2 & \cdots & v_n \end{bmatrix} \begin{bmatrix} e^{\lambda_1 t} & & & &\\ & e^{\lambda_2 t} & & \\ & & \ddots & &\\ & & & e^{\lambda_n t} \end{bmatrix} \begin{bmatrix} z_1(0) \\ z_2(0) \\ \vdots \\ z_n(0) \end{bmatrix} \\ = v_1 e^{\lambda_1 t}z_1(0) + v_2 e^{\lambda_2 t}z_2(0) + \cdots + v_n e^{\lambda_n t}z_n(0) \\ = v_1 z_1(t) + v_2 z_2(t) + \cdots + v_n z_n(t) \;\cdots\cdots(6)$$ \(z_i(t)\)をモードといい、式(6)をモード展開という。
※モードに関しては、13. モード展開と伝達関数行列を参照願います。
固有値が複素数のときのシステムのインパルス応答
固有値が共役複素数となるシステムのインパルス応答を求める。なお、システム行列\(A =\begin{bmatrix} 1 & 1 \\ -5 & -3 \end{bmatrix} \)、 入力行列 \(B = \begin{bmatrix} 1 \\ 1 \end{bmatrix} \)、 出力行列 \(C = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\) とする。
\(A\)の固有値は、$$|sI - A | = 0 \\ \left| \begin{bmatrix} s & 0 \\ 0 & s \end{bmatrix} -\begin{bmatrix} 1 & 1 \\ -5 & -3 \end{bmatrix} \right| \\ = \left| \begin{bmatrix} s-1 & -1 \\ 5 & s+3 \end{bmatrix} \right| \\ = s^2 +2s + 2 = 0$$ よって、固有値は、\(-1 \pm j\)である。
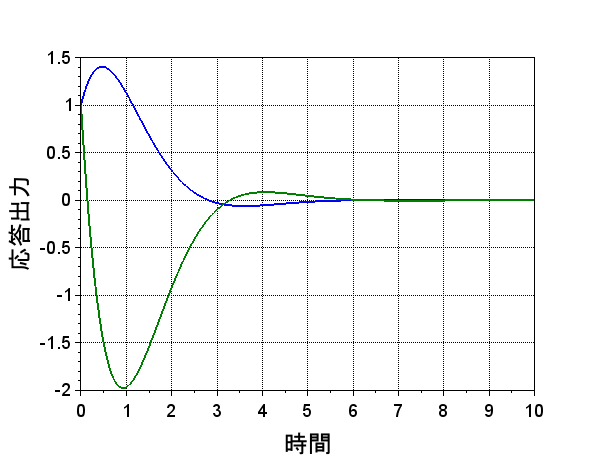
図5に、Scilabで計算したインパルス応答を示す。システム行列\(A\)の固有値が共役複素数なので、インパル応答は、振動的になる。また、固有値の実部が負であるため、インパル応答は0に収束する。つまり、このシステムは安定である。
Scilabによるシステムのインパルス応答計算
//固有値とインパルス応答
clear; clf;
i=%i;
//システムの定義
A = [1 1 ; -5 -3];
B = [1 ; 1]
C = [1 0; 0 1];
disp(spec(A));//固有値の表示
sysP=syslin('c', A, B, C);
t=0:0.01:10;
//インパル応答の計算
y=csim('impulse', t, sysP);
scf(0); plot(t',y');