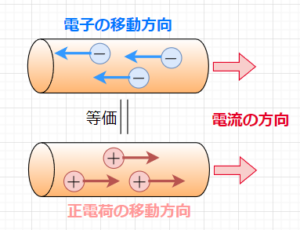
4. 電位、電圧（電位差）

電位とは、ある地点における電荷の持つエネルギーのことを指す。電位は、基準点における電位を0と定義し、その基準点からの距離と電荷によって決まる。電位の単位はボルト\( [V]\)であり、\(1\;[V]\)は\(1\;[C]\)の電荷を\(1\;[J]\)分の仕事をして運ぶのに必要な電位差と定義される。

電位

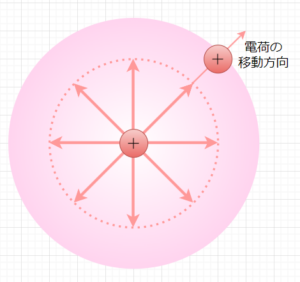
電界においても重力場と同じように、電気的な位置エネルギーの高い点、低い点がある。（重力場では、高いところにある質量は大きな位置エネルギーを持つ。）電気的位置エネルギーの高・低が電位の高・低である。

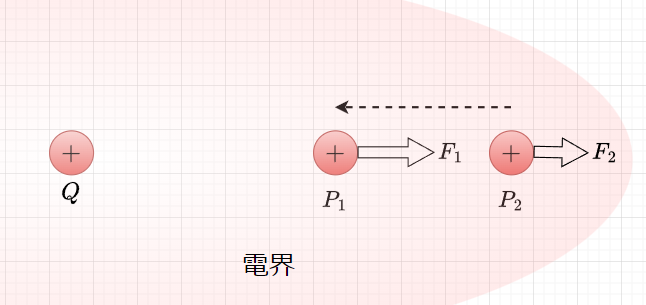
図１のよう電荷\(Q\)から異なる距離の点\(P_1,\;P_2\)を考える。それぞれの点で正電荷に働く静電力は、点\(P_1\)から点\(P_2\)の方向に働く。このとき、点\(P_2\)から点\(P_1\)まで正電荷を運ぼうとすると、電荷に働く静電力に逆らって運ばなければならない。従って、外部から運ぶためのエネルギー（仕事）を加えなければならない。従って、点\(P_1\)の方が\(P_2\)より電気的な位置エネルギーが高いことになる。電界中の電気的位置エネルギーの大きさは、単位正電荷\(+1\;[C]\)を静電力に逆らって運ぶときに要する仕事で表し、この電気的位置エネルギー（\([J/C]\)）の大きさで電位の大きさを定める。すなわち、電界中のある点の電位とは、「静電力の及ばない、電界の強さが０と見なせる無限遠点から単位正電荷（\(+1\;[C]\)）をある点まで運んでくるのに要する仕事\([J]\)」で、単位正電荷のもつ仕事量\([J/C]\)と定義される。また、実用的には、単位として\([V]\)を用いる。つまり、\([J/C] = [V]\)である。これは、電気での仕事量は、\([J] =[W][s] = [A][V][s]\)であり、\([C] = [A][s]\)なので、\([J/C] = \frac{[A][V][s]}{[A][s]} = [V]\)となると考えればよい。また、電位は位置のエネルギーなので、ベクトル量である電界と異なり、スカラ量（大きさのみで方向を持たない量）である。

電圧（電位差）

２つの異なる点\(A,\;B\)のそれぞれの電位を\(V_A,\;V_B\)とするとき、\(V_A -V_B\)を\(AB\)間の電位差、電圧という。$$V_{AB} =V_A - V_B$$と表し、\(V_{AB}\)が正なら\(A\)点の電位が\(B\)点の電位より高く、負ならば、\(A\)点の電位が\(B\)点の電位より低いことになる。

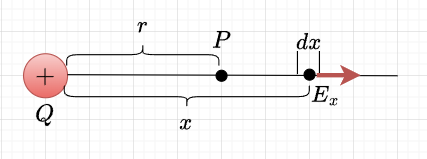
真空中において、図２のように、点電荷\(Q\;[C]\)から\(r\;[m]\)離れた点\(P\)の電位は、\(Q\)から任意の距離\(x\)のところに微小距離\(dx\)をとると、\(dx\)における電界の強さは、$$E_x = \frac{Q}{4 \pi \epsilon_0 x^2} \;[V/m]$$であるから、\(dx\)区間で単位正電荷を電界に逆らって運ぶのに要する仕事\(dw\)は、$$dw = - E_x dx \;[J]$$と書ける。従って、単位正電荷を無限遠点から\(P\)点まで運ぶのに要する仕事\(W\)は、$$W = - \int_{\infty}^r E_x dx = - \int_{\infty}^r \frac{Q}{4 \pi \epsilon_0 x^2} dx = - \frac{Q}{4 \pi \epsilon_0} \left[ -\frac{1}{x} \right]_{\infty}^r \\ = \frac{Q}{4 \pi \epsilon_0} \left( \frac{1}{r} - \frac{1}{\infty} \right) = \frac{Q}{4 \pi \epsilon_0 r} \;[J]$$となる。これが\(P\)点の電気的位置エネルギーを表しているから、定義より\(P\)点の電位は、$$V_P = \frac{Q}{4 \pi \epsilon_0 r} \;[V]$$である。
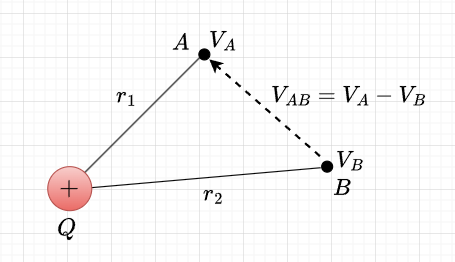
次に、２点間の電圧（電位差）を考える。図３のように、\(Q\)から\(r_1\)離れた\(A\)点と\(r_2\)離れた\(B\)点間の電圧は、$$V_{AB} = V_A - V_B = \frac{Q}{4 \pi \epsilon_0} \left(\frac{1}{r_1} - \frac{1}{r_2}\right) \;[V]$$と表せる。