7. 磁気の性質
磁気の基本的な性質は、磁石が互いに引き合ったり反発したりする現象に見られる。磁石にはN極とS極があり、異なる極同士は引きつけ合い、同じ極同士は反発する。この性質は、磁性と呼ばれ、磁場に反応する性質を指す。磁気の性質は以下である。
・磁気双極子: 磁石には必ずN極とS極の両方が存在する。(磁気単極子の存在は未確認)
・磁力線: 磁石の周りには、磁力線が存在する。磁力線は、N極からS極へと向かっている。
・磁場:磁力線が存在する空間を磁場と呼ぶ。
・磁荷:磁荷は、磁極が帯びている磁気の量を表す。N極の磁荷は正、S極の磁荷は負と定義する。正の磁荷と負の磁荷は引き合い、同じ種類の磁荷は反発する。
・磁性:磁性とは、物質が磁場に反応する性質のことである。磁性を持つ物質には、鉄、ニッケル、コバルト、アルニコ、フェライトなどがある。
磁気
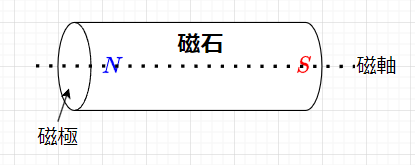
磁石が鉄片などを引き付ける性質(磁性)の根源を磁気という。また、鉄片などを磁石にすることを磁化という。図1に示すように、磁石の両端が最も磁性が強く、この部分を磁極という。両磁極を結ぶ線を磁軸という。1つの磁石にはN極とS極の2つの磁極が必ずあり、磁気双極子を形づくっている。(磁気単極子の存在は、理論上提唱されているが、未確認である。)
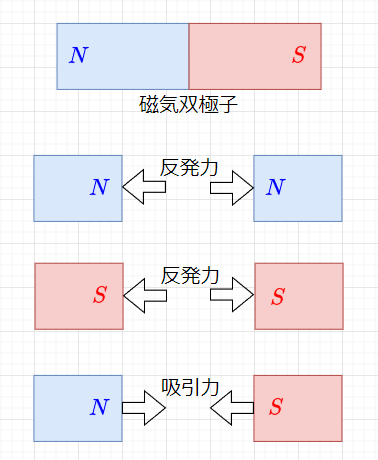
磁気の重要な性質は、図2に示すように磁極間で作用する磁気力である。磁極間には、N極とN極、S極とS極の同種の磁極間では反発力、N極とS極の異種の磁極間には吸引力が働く。磁極の強さは、静電気における電荷に対応して磁荷\(m\)を使って考える。磁極の強さの単位は、SI単位系においては、\([Wb]\)(ウェーバー)を用いる。(組立単位で表すと\([V\cdot s]\)(ボルト秒)である。)
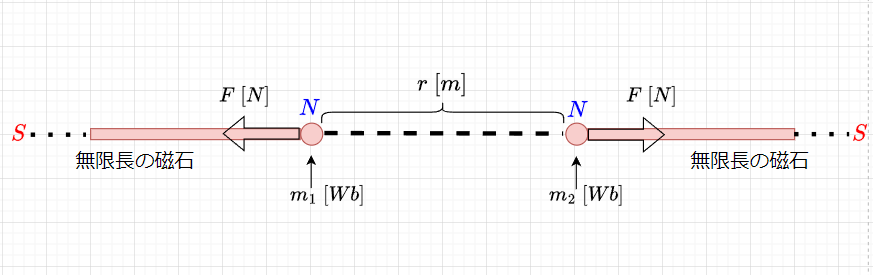
図3のように、無限長の磁石を想定して、N極同士を対向して配置することを考える。この場合、対向した位置に点磁極\(m_1,\;\;m_2\)が置かれたと考えることができる。この磁極の間には、静電力の場合と同様にクーロンの法則が成立し、磁気力\(F\)が働く。真空中では、$$F = k \cdot \frac{m_1 m_2}{r^2} \;[N] \\ k = \frac{1}{4 \pi \mu_0} $$である。
つまり、「点磁極間に働く磁気力は、2つの磁極の強さの相乗積に比例し、磁極間の距離の2乗に反比例する」である。真空以外の媒質中では、$$ k = \frac{1}{4 \pi \mu} = \frac{1}{4 \pi \mu_0 \mu_s}$$となる。ここで、\(\mu_0\)は真空の透磁率で\(\mu_0 = 4 \pi \times 10^{-7}\)、\(\mu\)は真空以外の一般の媒質の透磁率、また、\(\mu_s = \mu / \mu_0\)は比透磁率である。なお、点磁極は理論上考えたものであることに注意されたい。
磁界の強さ
磁気力の作用が及ぶ空間を磁界(磁場)という。磁界を定量的に表すのに磁界の強さが電界の強さと同様に定義される。
磁界の強さの定義と単位
磁界の強さは、「磁界中の任意の一点に単位磁極\(+1\;[Wb]\)を置いたとき、これに働く磁気力の大きさをその点の磁界の強さ(大きさ)とし、磁気力の方向を磁界の方向とする」と定義される。すなわち、磁界の強さは単位磁極の強さ当たりの磁気力で表す。磁界の強さの記号には一般に\(H\)を用いる。磁界の強さの単位は、定義から\([N/Wb]\)であるが、実用的には\([A/m]\)が用いられる。(磁界の強さには、電流が大きく関与していることを意味する。)また、磁界の強さは大きさと方向をもつベクトル量である。
磁界の強さの単位
磁界の強さの単位は、定義から\([N/Wb]\)であるが、\([Wb]=[V\cdot s]\)であり、\([N] = [J/m] = [\frac{V\cdot A \cdot s}{m}]\)なので、\([N/Wb] = \frac{[V \cdot A \cdot s/m]}{[V \cdot s]} = [A/m]\)となる。
磁界中の磁極に働く磁気力
磁界中に磁極を置いたとき、磁極に働く磁気力を考える。磁界中に\(m\;[Wb]\)の点磁極に\(F\;[N]\)の磁気力が働いたとすると、その点の磁界の強さは定義より、$$H = \frac{F}{m} \;[A/m]$$である。従って、磁界\(H \;[A/m]\)の中に、点磁極\(m \;[Wb]\)を置くと$$F = m H \;[N]$$の磁気力が作用することになる。
点磁極の周りの磁界の強さ
図4のように、\(m\;[Wb]\)の点磁極があったとし、この点磁極\(m\)から\(r\;[m]\)離れた点の磁界の強さ\(H\)を求める。\(P\)点に\(\Delta m \;[Wb]\)の微小磁極を置いたとすると、この\(\Delta m\)に働く磁気力\(\Delta F\)は、クーロンの法則より、$$\Delta F = \frac{m \cdot \Delta m}{4 \pi \mu_0 r^2} \;[N]$$である。従って、磁界の強さ\(H\)は、$$H = \frac{\Delta F}{\Delta m} = \frac{m}{4 \pi \mu_0 r^2}\;[A/m]$$となる。
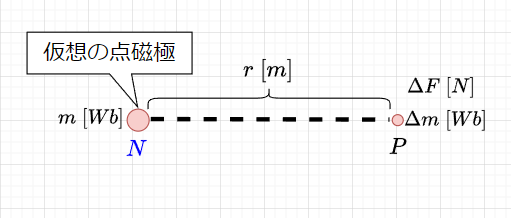
※点磁極を仮想して磁界の強さを求めるのは、理論上のものであって、実際には理想的な点磁極は存在しないとされていることに注意が必要である。
磁力線と磁束
電界の状態として、電気力線や電束を仮想したように、磁界の状態として、磁力線や磁束を仮想する。磁石上にガラス板などを置き、その上に砂鉄を一様に散布すると、図5のように砂鉄は磁界による磁気力を受けて、直線や曲線状に配列する。この直線、曲線は、磁石の周辺の磁界の方向、分布を表していると考えられる。磁力線は以下のように定義される。
(1)磁力線はN極から始まりS極に終わる。
(2)磁力線の方向で、磁界の方向を表す。
(3)磁力線は単位面積当たりの磁力線数(磁力線密度)と磁界の強さは等しい。
磁力線数
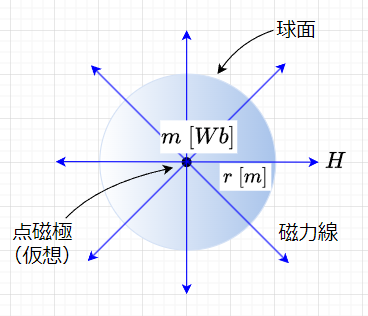
図6のように、\(m\;[Wb]\)の磁極から発する磁力線数を考える。真空中での任意の半径\(r\;[m]\)の球面上の磁界の強さは、$$H=\frac{m}{4 \pi \mu_0 r^2} \;[A/m]$$である。球面上の磁界の強さは一定で、磁力線密度に等しいから、\(m\;[Wb]\)から出る磁力線数を\(N\)とすると、\(N\)は磁力線密度×面積なので、$$N = \frac{m}{4 \pi \mu_0 r^2} \times 4 \pi r^2 = \frac{m}{\mu_0}$$となる。

引用元:https://www.isee.nagoya-u.ac.jp/50naze/chijiki/9.html
透磁率\(\mu \)の一般の媒質中では、$$N = \frac{m}{\mu} = \frac{m}{\mu_0 \mu_s}$$となる。
図6では、仮想的な点磁極で考えているが、磁気双極子で考えてもそれぞれの磁極において\(m\;[Wb]\)の磁極から\(m/ \mu_0\)の磁力線が発すると考えられる。
磁束と磁束密度
磁束\(\phi\)を以下のように定義する。
(1)磁束\(\phi\)は、磁石の内部、外部に関わらず連続した線である。磁石内部ではS極からN極へ、磁石外部ではN極からS極へ向かう。
(2)磁束\(\phi\)の単位は磁極の強さと同じ\([Wb]\)である。
(3)磁極の強さ\(m\;[Wb]\)の磁石には\(m\;[Wb]\)の磁束が通る。つまり、\(\phi = m \;[Wb]\)である。
磁極の強さ\(m\;[Wb]\)から発する磁力線数\(N\)と磁束\(\phi\)は、真空中では、$$N = \frac{m}{\mu_0} \;\;\;\;\;\; \phi = m$$である。従って、$$\phi = \mu_0 N \;[Wb]$$である。また、透磁率\(\mu\)の媒質中では、\(\phi = \mu N = \mu_0 \mu_s N\)となる。
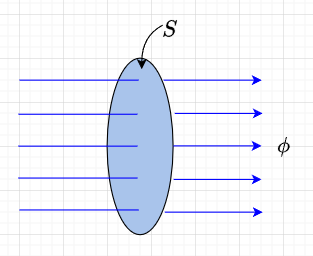
図7のように、面積\(S\;[m^2]\)を通る磁束を考えると、磁束密度\(B\)(単位面積当たりの磁束)は、$$B = \frac{\phi}{S} = \mu_0 \cdot \frac{N}{S}$$となる。磁力線密度\(N/S\)は磁界の強さ\(H\)なので、磁束密度\(B\)は、$$B = \mu_0 H \;[Wb/m^2]$$となる。なお、磁束密度\(B\)の単位は、定義からは\([Wb/m^2]\)であるが、実用上は\([T]\)(テスラ)を使用する。また、透磁率\(\mu\)の媒質中では、\(B= \mu H = \mu_0 \mu_s H \;[T]\)である。