33. 制御系の設計例
古典制御理論の範囲での制御系設計では、ゲイン補償器、位相進み補償器、位相遅れ補償器(もしくは積分補償器)を使用するか、PID制御を使用する場合が多い。ここでは、ゲイン補償器、位相進み補償器、位相遅れ補償器を直列に接続した単位フィードバック制御系の具体例をみる。
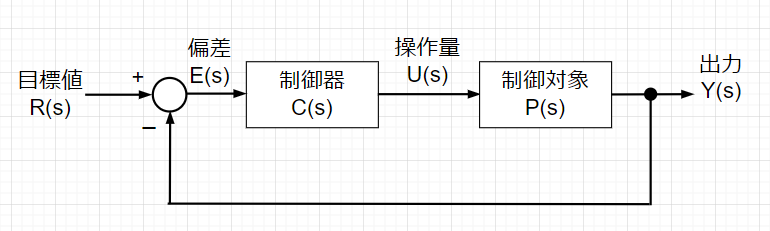
制御対象は、$$P(s)=\frac{1}{s(s+1)(s+3)}$$とする。
制御仕様は以下とする。
・位相余裕\(p_m = 45^{°}\)以上、ゲイン余裕\(g_m=12dB\)以上、ゲイン交差周波数\(\omega_c\)はできるだけ高く
・定常位置偏差\(e_p=0\)、定常速度偏差\(e_v=0.5\)以下
制御対象\(P(s)\)の特性方程式は、\(s(s+1)(s+3)=0\)で、極は、\([0, -1,-3]\)なので、\(P(s)\)は不安定である。また、\(P(s)\)は\(\frac{1}{s}\)を持っているので、制御器\(C(s)\)の零点で\(P(s)\)の極\([0]\)を相殺しない限りにおいて(一般に制御器\(C(s)\)が完全な微分要素\(s\)を持つことはないので、この極零相殺は無いと考えてよい)、開ループ伝達関数\(L(s) = C(s)P(s)\)は1型系である。従って、内部モデル原理より定常位置偏差\(e_p=0\)である。
*ゲイン補償器(設計の詳細は「ゲイン補償器」を参照)
ゲイン\(K\)を直列に接続して単位フィードバック制御系にすると、閉ループ伝達関数は、$$T(s)=\frac{KP(s)}{1+KP(s)}$$となり、\(K\)の値によっては制御系を安定にできる。特性方程式は\(1 + KP(s) = 0\)なので、\(K\)(ゲイン補償器)の範囲は、ラウスの安定判別から、\(0 \lt K \lt 12\) となる。
*位相進み補償器(設計の詳細は「位相進み補償器」を参照)
次のパラメータの位相進み補償器を使う。$$ \alpha =14.38 \enspace \enspace T=0.11$$ $$C1(s) = \frac{1+1.58s}{1 + 0.11s}$$
この位相進み補償器の主な働きは、ゲイン交差周波数近傍の位相を進めることで位相余裕を大きくして、安定度を高めるとともに、ゲイン交差周波数を高くして速応性を向上させることにある。
*位相遅れ補償器(設計の詳細は「位相遅れ補償器」を参照)
次のパラメータの位相遅れ補償器を使う。$$ \beta = 0.3886 \enspace \enspace T=13.62$$ $$C2(s) = \frac{2(1 + 5.18s)}{1 + 13.62s}$$
この位相遅れ補償器の主な働きは、低域の利得を上げることで定常速度偏差を抑制することにある。なお、ゲイン交差周波数近傍の利得、位相には影響を与えない低域に設定する。
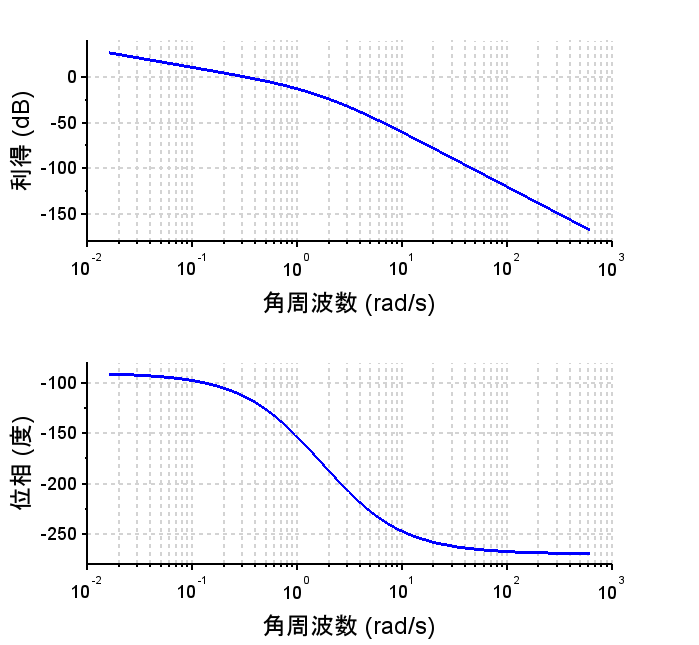
\(L(s)\),\(T(s)\),\(S(s)\):ゲイン補償のみ
\(L1(s)\),\(T1(s)\),\(S1(s)\):ゲイン補償+位相進み補償
\(L2(s)\),\(T2(s)\),\(S2(s)\):ゲイン補償+位相進み補償+位相遅れ補償
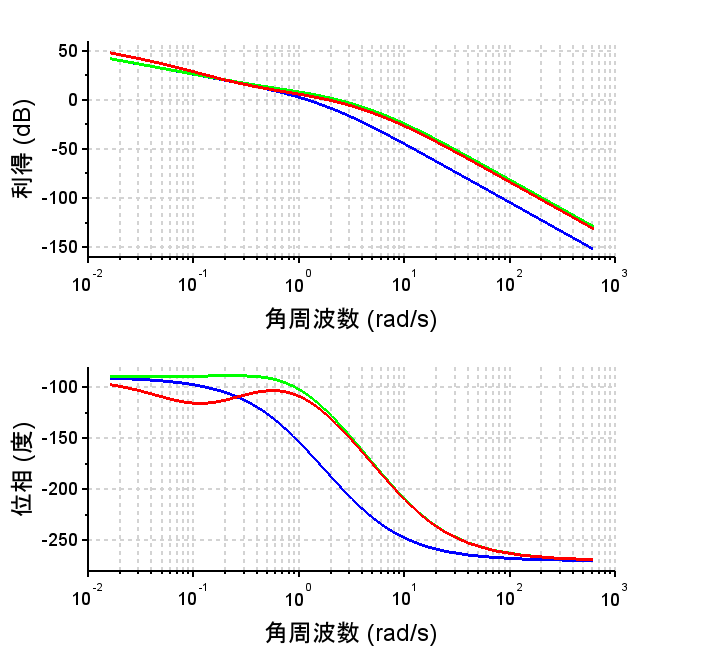
\(L(s)\):青、\(L1(s)\):緑、\(L2(s)\):赤
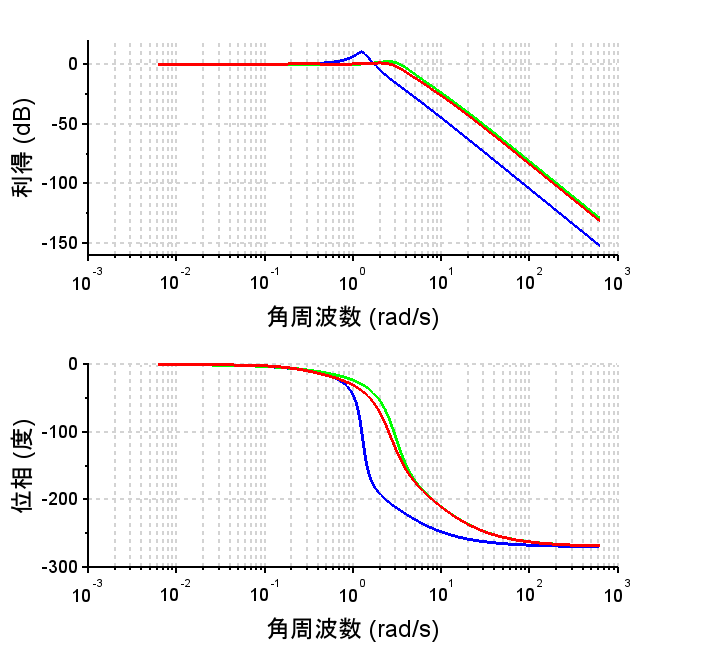
\(T(s)\):青、\(T1(s)\):緑、\(T2(s)\):赤
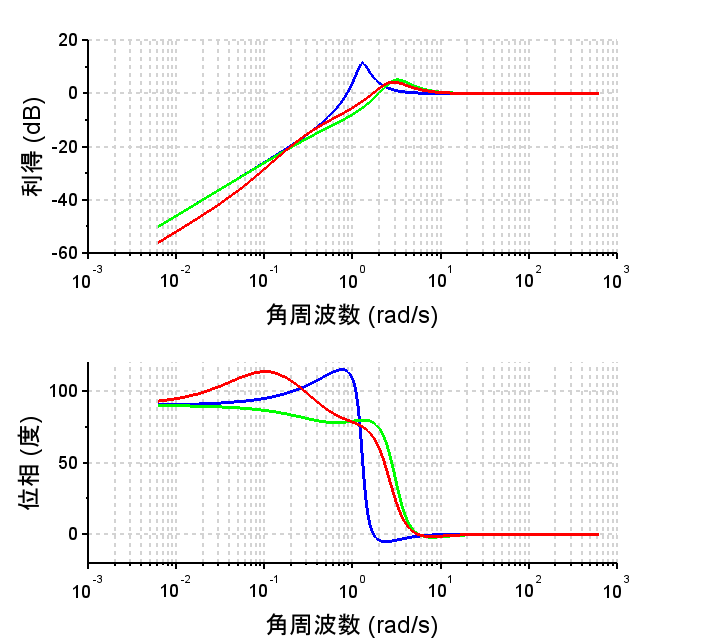
\(S(s)\):青、\(S1(s)\):緑、\(S2(s)\):赤
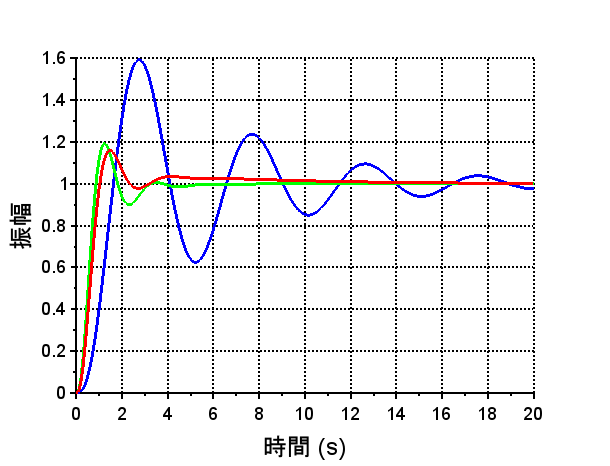
\(T(s)\):青、\(T1(s)\):緑、\(T2(s)\):赤
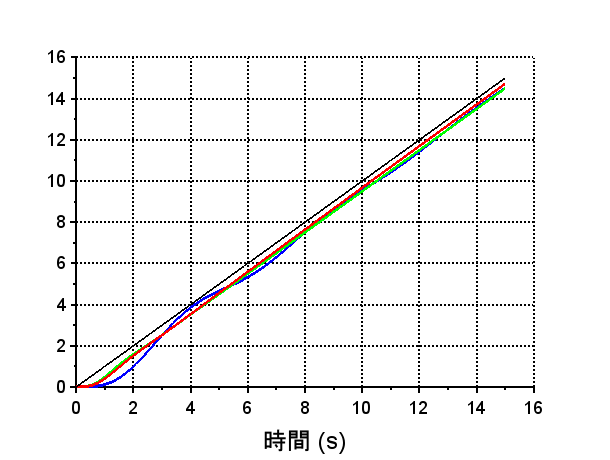
\(T(s)\):青、\(T1(s)\):緑、\(T2(s)\):赤
ランプ信号:黒
制御器設計例
(Scilabスクリプト)
開ループ伝達関数(\(L2(s)\))より、位相余裕、利得余裕とも制御仕様を満たしていることが分かる。
ステップ応答の比較では、\(T1(s)\)、\(T2(s)\)とも良好である。
ランプ応答の比較では、\(T2(s)\)で定常速度偏差\(e_v=0.5\)以下を達成できている。
感度関数\(S2(s)\)を見ると低域において十分に利得が低下しており、低域において偏差を抑制する働きが強いことが分かる。
//制御系の設計例
clear; clf();
s=%s;
//制御対象P
P=1/(s*(s+1)*(s+3));
Ps=syslin('c',P);
scf(0);
bode(Ps,10^-3,10^2,'rad');
//ゲイン補償器K
K=6;
L=K*P;
Ls=syslin('c',L);
T=L/(1+L);
Ts=syslin('c',T);
//ゲイン補償K+位相進み補償器C1
C1=(1+1.58*s)/(1+0.11*s);
C1s=syslin('c',C1);
L1=K*C1*P;
L1s=syslin('c',L1);
T1=L1/(1+L1);
T1s=syslin('c',T1);
//位相遅れ補償器C2
C2=(2*(1+5.18*s))/(1+13.62*s);
C2s=syslin('c',C2);
//ゲイン補償K+位相進み補償器C1+位相遅れ補償器C2
L2=K*C1*C2*P;
L2s=syslin('c',L2);
T2=L2/(1+L2);
T2s=syslin('c',T2);
//開ループ伝達関数L(s) 比較
scf(1);
bode([Ls;L1s;L2s],10^-3,10^2,'rad');
//閉ループ伝達関数T(s) 比較
scf(2);
bode([Ts;T1s;T2s],10^-3,10^2,'rad');
//感度関数S(s)比較
S=1/(1+L);
Ss=syslin('c',S);
S1=1/(1+L1);
S1s=syslin('c',S1);
S2=1/(1+L2);
S2s=syslin('c',S2);
scf(3);
bode([Ss;S1s;S2s],10^-3,10^2,'rad');
//ステップ応答の比較
t=0:0.1:20;
scf(4);
y=csim('step',t,Ts);
y1=csim('step',t,T1s);
y2=csim('step',t,T2s);
plot2d(t,y,2);xgrid;
plot2d(t,y1,3);
plot2d(t,y2,5);
//ランプ応答の比較
t=0:0.1:15;
scf(5);
y=csim(t,t,Ts);
y1=csim(t,t,T1s);
y2=csim(t,t,T2s);
plot2d(t,y,2);xgrid;
plot2d(t,y1,3);
plot2d(t,y2,5);
plot2d(t,t,1); /*目標値(ランプ信号)の描画*/


“33. 制御系の設計例” に対して1件のコメントがあります。
コメントは受け付けていません。