1-1. 離散時間制御系の構成(演習)
連続時間システムから離散時間システムへの変換
連続時間システムが微分方程式$$\frac{dy}{dt} = \alpha y + \beta u \;\; \cdots (1)$$で与えられるとき、このシステムをディジタルシステムに変換する。
式(1)の自由システムは、$$\frac{dy}{dt} = \alpha y$$で、変数分離形なので、$$\frac{dy}{y} = \alpha dt$$となり、両辺を積分すると、$$\ln y = \alpha t + c' \;\;\;\;\;\; y = e^{\alpha t}c \;\;\;\cdots\cdots (2)$$ (\(c \):積分定数)を得る。\(c\)を時間関数と見なして、微分すると、$$\frac{dy}{dt} = \alpha e^{\alpha t} c + e^{\alpha t} \frac{dc}{dt} = \alpha y + e^{\alpha t} \frac{dc}{dt}$$となる。式(1)と比較して、$$\frac{dc}{dt} = e^{- \alpha t} \beta u$$なので、これを積分すると、$$c (t) = \int_0^t e^{-\alpha \tau}\beta u(\tau) d\tau + c''$$ (\(c''\):積分定数)となる。これを式(2)に代入すると、$$y(t) = c'' e^{\alpha t} + \int_0^t e^{\alpha (t - \tau)} \beta u (\tau) d \tau$$である。\(t=0\)とおけば、\(c'' = y(0)\)なので、式(1)の一般解は、$$y(t) = e^{\alpha t} y(0) + \int_0^t e^{\alpha (t - \tau)} \beta u (\tau) d \tau \;\;\;\cdots \cdots (3)$$である。式(3)をディジタルシステムに変換するには、\(t = k T + T\)(\(k = 0,1,2,\cdots\))とおくと 、$$y(k T + T) = e^{\alpha T} e^{k \alpha T} y(0) + e^{\alpha T} \int_0^{k T} e^{\alpha (k T - \tau)} \beta u(\tau) d \tau + e^{\alpha T} \int_{k T}^{k T + T} e^{\alpha(k T - \tau)} \beta u(\tau) d \tau$$となる。ここで、0次ホールドを仮定すれば、サンプリング間隔で、$$u(\tau) = u(k T) ,\;\;\;\; (kT \le \tau \lt (k T+T) )$$であり、
$$y(k T) = e^{\alpha k T} y(0) + \int_0^{k T} e^{\alpha (k T - \tau)} \beta d \tau \cdot u(k T)$$なので、
$$ y(k T +T) = e^{\alpha T} y(k T) +e^{\alpha T} \int_{k T}^{k T + T} e^{\alpha(k T - \tau)} \beta d \tau \cdot u(k T)$$と書ける。さらに、$$e^{\alpha T} \int_{k T}^{k T + T} e^{\alpha(k T - \tau)} \beta d \tau = \beta \int_{k T}^{k T + T} e^{\alpha (k T + T - \tau)} d \tau $$ \(\sigma = k T + T - \tau\)と変数変換すると、$$-\beta \int_0^T e^{\alpha \sigma} d \sigma = -\frac{\beta}{\alpha}( 1 - e^{\alpha T})$$となる。ここで、$$a = e^{\alpha T} , \;\;\;\; b = -\frac{\beta}{\alpha}( 1 - e^{\alpha T})$$とおくと、$$y(k T + T) = a y(k T) + b u(k T)$$と離散時間システムが求まる。また、コンピュータ内部での計算を考え、\(T\)を省略すると、$$y(k + 1) = a y(k) + b u(k)$$と表現できる。(サンプリング間隔\(T\)の影響は、パラメータ\(a,\;b\)に含まれている。)
離散時間システムによるタンク内の湯温度の制御問題
(1)湯温度制御システムの状態方程式とその離散化
ニュートンの冷却の法則によると、液体が放射によって失う総エネルギー量は、その液体と周囲の温度差に比例する。温度差を\(y(t)\)とすると、$$\frac{dy(t)}{dt} = \alpha y(t) + \beta u(t) \;\;\; \cdots (1)$$が成立する。\(u(t)\)は加熱エネルギーで、\(u(t)=0\)とすれば、冷却の法則を表す。\(\alpha\)(\(\alpha \lt 0\))は冷却係数、\(\beta\)(\(\beta \gt 0\))は、加熱エネルギーが温度上昇エネルギーに変換される割合を表す。サンプリング間隔を\(T\)と仮定して、$$y(k + 1) = a y(k ) +b u(k ) \;\;\; \cdots (2)$$と離散化する。ただし、$$a = e^{\alpha T} , \;\;\; b = - \frac{\beta}{\alpha} ( 1 - e^{\alpha T})$$である。式(1)を1次の線形連続時間システム、式(2)をそれと等価な1次の線形離散時間システムと呼ぶ。\(u = 0\)で\(\alpha \lt 0\)であれば、\(a \lt 1\)なので、式(1)、(2)ともに安定である。式(2)が離散化した制御対象の動特性を表しており、加熱エネルギー\(u\)を調節することで、湯温\(y\)を制御できることを示している。
ニュートンの冷却の法則
物体が放射によ って失う熱量は、その物体と周囲との温度差に比例する。この法則は次の式で表される。
$$\frac{dy}{dt}=−\alpha (y−y_{env})$$ここで、
・\(y\)は物体の温度
・\(y_{env}\) は周囲環境の温度
・\(\alpha\)は冷却定数(物体と環境に依存する)
この式は、時間とともに物体の温度が指数関数的に減少し、最終的に環境温度に達することを示している。
(2)離散時間システムにおいて、温度を目標値\(r\)(一定値)に一致させる制御器を設計する
式(2)の離散時間システムに対して、$$u(k) = - f_1 y(k) + f_2 r$$の制御器を構成する。式(2)に代入すると、$$y(k +1) = a y(k) + b \{- f_1 y(k) + f_2 r \} = ( a - b f_1)y(k) + b f_2 r \;\;\cdots (3)$$となる。このとき、\(y(k) \rightarrow y'\) (\(y'\)は一定値)になることが、温度を一定値にする条件の一つなので、\(f_1\)は\(|a - b f_1| \lt 1\)を満足しなければならない。この場合、\(k \rightarrow \infty\)において、\(y(k+1) = y(k)\)となるので、$$(1 - a + b f_1) y' = b f_2 r$$が成立し、\(y' = r\)であるためには、\(f_1,\;f_2\)は$$\frac{b f_2}{1 - a + b f_1} = 1$$を満足しなければならない。従って、制御器は、$$u(k) = -f_1 y(k) + \frac{1 - a + b f_1}{b} r$$となる。式(3)をZ変換すると、$$zY(z) = ( a - b f_1)Y(z) + b f_2 r \frac{z}{z -1}$$ なので、$$Y(z) = b f_2 r \frac{z}{z-1} \cdot \frac{1}{z - (a - b f_1)}$$である。最終値定理より、$$\lim_{k \rightarrow \infty} y(k) = \lim_{z \rightarrow 1} (1 - z^{-1})Y(z) = \lim_{z \rightarrow 1} b f_2 r \frac{1}{z - (a-b f_1)} = \frac{b f_2 r}{1 - a + b f_1}$$となる。\(f_1,\;f_2\)を\(\frac{b f_2}{1 - a + b f_1} = 1\)を満足するように選定するので、$$\lim_{k \rightarrow \infty} y(k) = r$$となる。
しかしながら、この制御器では\(y \rightarrow r\)が達成できない場合がある。このことは以下による。式(1)から\(u-y\)間の伝達関数\(G(s)\)を求める。式(1)の両辺を初期値0でラプラス変換すると、$$sY(s) =\alpha Y(s) + \beta U(s)$$よって、$$G(s) = \frac{Y(s)}{U(s)} = \frac{\beta}{s - \alpha}$$となり、インパルス応答\(g(t)\)は、$$g(t) = \beta e^{\alpha t}$$である。\(\alpha \lt 0\)であれば、このシステムは安定である。しかし、\(G(s)\)からこのシステムは0型なので、内部モデル原理より、定常位置偏差を0にすることはできない。(前述の「\(y \rightarrow r\)が達成できない。」のこと。)定常位置偏差を0にするには、制御器に積分要素が必要である。
積分要素を入れた制御器として、$$u(k) = -f_1 y(k) + f_2 r + f_3 z(k) ,\\ z(k + 1) = z(k) +\{ r - y(k) \} \;\;\; \cdots (4)$$を考える。これより、$$y(k+1) = a y(k) + b u(k) =a y(k) + b \{- f_1 y(k) + f_2 r + f_3 z(k) \} ,\\ y(k +1) = (a - b f_1)y(k) + b f_3 z(k) +b f_2 r \;\;\; \cdots (5)$$なので、閉ループ系は、$$\begin{bmatrix} y(k+1) \\ z(k+1) \end{bmatrix} = \begin{bmatrix} a - b f_1 & b f_3 \\ -1 & 1 \end{bmatrix} \begin{bmatrix} y(k) \\ z(k) \end{bmatrix} + \begin{bmatrix} b f_2 \\ 1 \end{bmatrix} r \;\;\cdots (6)$$となる。式(6)の特性方程式は、$$|\lambda I - A| = \lambda^2 - (1 + a - b f_1)\lambda + a - b f_1 +b f_3 = 0$$なので、この閉ループ系を安定にする(すなわち\(|\lambda| \lt 1\)とする)\(f_1,\;f_3\)が存在する。従って、そのような\(f_1,\;f_3\)を選定すると、\(k \rightarrow \infty\)で$$\begin{bmatrix} y(k) \\ z(k) \end{bmatrix} \rightarrow \begin{bmatrix} y' \\ z' \end{bmatrix}$$となる。(\(y', \; z'\)は定数)\(k \rightarrow \infty\)で、\(y',\;z'\)が一定値となるので、式(4)より、\(y' = r\)となることがわかる。
Scilabによるシミュレーション
*Scilabスクリプト
//タンクの湯温制御(演習)
clear; clf;
z=%z;e=%e;
a=0.8; b=1.0;
//積分要素が無い場合
f1=0.5; f2=0.3; f3=0;
A1=[a-b*f1 b*f3 ; -1 1];
B=[b*f2 ; 1];
c=[1 0];
Tz1=syslin('d',A1,B,c);
Tzz1=ss2tf(Tz1);
//ステップ応答
r = [1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ];
y1 = flts(r,Tzz1);
//積分要素が有る場合
f1=0.5; f2=0.3; f3=0.2;
A2=[a-b*f1 b*f3 ; -1 1];
B=[b*f2 ; 1];
c=[1 0];
Tz2=syslin('d',A2,B,c);
Tzz2=ss2tf(Tz2);
//ステップ応答
y2 = flts(r,Tzz2);
//1つのウィンドウにy1,y2をプロット
scf(0);plot(y1,'-x');plot(y2,'-o');
※r=[1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]とすれば、インパルス応答が求まる。
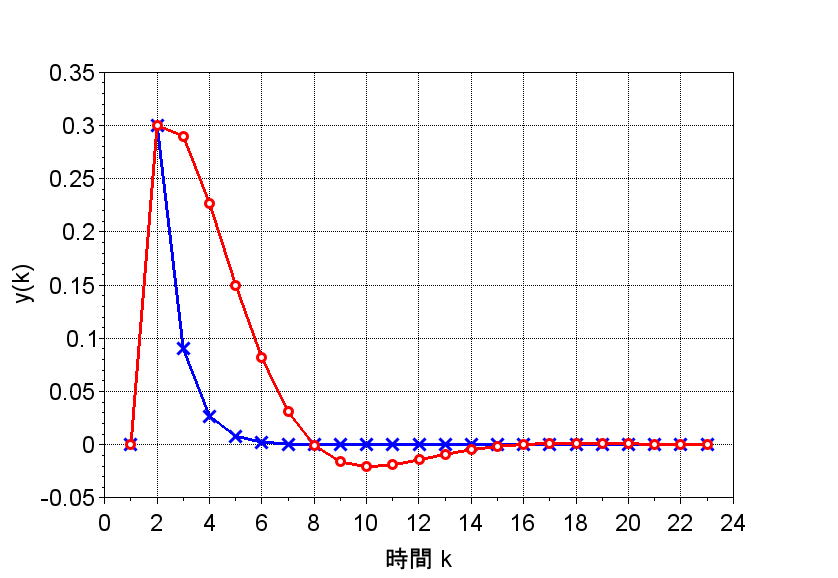
図1は、式(6)を基にしたインパルス応答のシミュレーション結果である。各パラメータは、\(a=0.8, \; b=1.0, \;f_1=0.5, \; f_2 =0.3\)としている。
「青」は積分要素が無い場合(\(f_3=0\))、「赤」は積分要素がある場合(\(f_3=0.2\))のインパルス応答特性で、いずれも安定に制御できることがわかる。
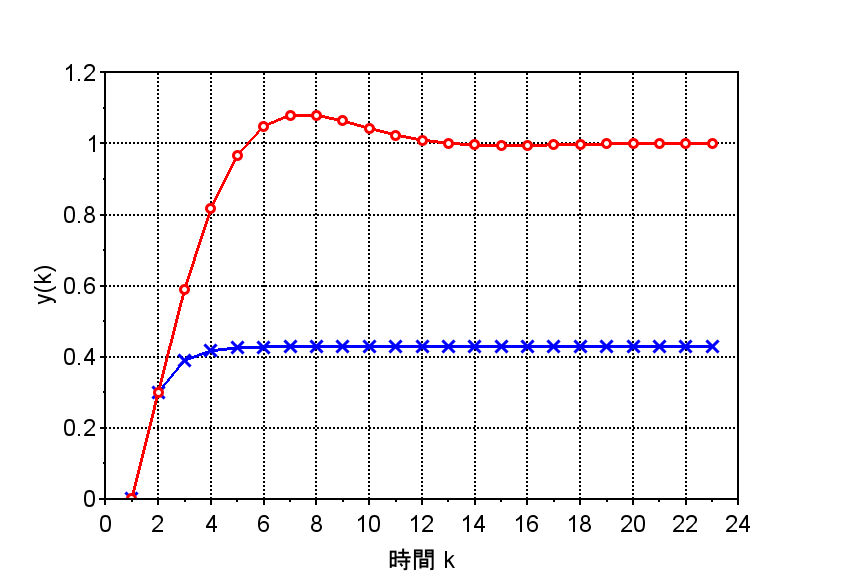
図2は、式(6)を基にしたステップ応答のシミュレーション結果である。各パラメータは、\(a=0.8, \; b=1.0, \;f_1=0.5, \; f_2 =0.3\)としている。
「青」は積分要素が無い場合(\(f_3=0\))、「赤」は積分要素がある場合(\(f_3=0.2\))のステップ応答特性である。積分要素が無い場合、目標値(\(r=1\))に到達できず、定常偏差が残ることがわかる。