5-1. 離散時間システムの応答(演習)
離散時間システムのインパルス応答
離散時間伝達関数が、$$G(z) = \frac{z + 0.3}{z^2 - 0.7z +0.1}$$のシステムのインパルス応答を求める。
解法1:$$G(z) = \frac{Y(z)}{U(z)} = \frac{z + 0.3}{z^2 - 0.7z +0.1}$$なので、$$Y(z)(z^2 - 0.7z +0.1) = U(z)(z + 0.3) \\ Y(z) (1 - 0.7z^{-1} + 0.1 z^{-2} = U(z)(z^{-1} + 0.3 z^{-2})$$である。これを逆Z変換すると、$$y(k) - 0.7y(k-1) + 0.1y(k-2) = u(k-1) + 0.3u(k-2) \\ y(k) = u(k-1) + 0.3u(k-2) + 0.7y(k-1) - 0.1y(k-2)$$となる。
インパルス応答は、\(u(0)=1\)それ以外では\(u(k)=0\)として、\(k \ge 0\)の範囲で逐次計算により、
・\(k=0\) のとき、\(y(0) = 0 \)
・\(k=1\)のとき、\(y(1) = u(0) + 0.7y(0) =1\)
・\(k=2\)のとき、\(y(2) = u(1) +0.3u(0) + 0.7y(1) - 0.1y(0) = 0 + 0.3 + 0.7=1.0\)
・\(k=3\)のとき、\(y(3) = u(2) +0.3u(1) + 0.7y(2) - 0.1y(1) = 0 + 0.7 - 0.1 = 0.6\)
\(\vdots\)
として求められる。
解法2:パルス伝達関数の一般形を、$$G(z) = \frac{b_0 z^n + b_1 z^{n-1} + \cdots + b_n}{z^n + a_1 z^{n-1} + \cdots a_n}$$として、一方、インパルス応答\(g(k)\)から、$$G(z) = \sum_{k=0}^{\infty} g(k) z^{-k}$$なので、この2式から、$$(1 + a_1 z^{-1} + \cdots + a_n z^{-n})\left\{g(0) + g(1)z^{-1} + \cdots \right\} = b_0 + b_1 z^{-1} + \cdots + b_n z^{-n}$$が成立する。両辺の同じ「べき」を比較すると、$$g(k) + a_1 g(k-1) + \cdots + a_n g(k-n) = b_k \;\;\;(k \le n) \\ g(k) + a_1 g(k-1) + \cdots + a_n g(k-n) = 0 \;\;\;(k \gt n) $$が得られる。この\(g(k)\)を求めれば、インパルス応答が求まる。
$$G(z) = \frac{z + 0.3}{z^2 - 0.7z +0.1}$$のとき、\(a_1 = -0.7 , \;a_2 = 0.1, \; b_0=0,\; b_1 =1,\;b_2=0.3\)であるから、\(g(1) = 1 , \;\; g(2) = 0.7g(1) + 0.3 =1\)となる。一般には、$$g(k) - 0.7 g(k-1) + 0.1g(k-2) = 0 \;\;(k \ge 3) \;\;\; \cdots (1)$$となる。いま、$$z^2 - 0.7z + 0.1 =0$$の根は、\(\lambda_1 = 0.5,\; \lambda_2 = 0.2\)なので、式(1)の一般解を$$g(k) = A_1 \lambda_1 ^k + A_2 \lambda_2 ^k$$とおく。\(k = 1, \; 2\)とすると、\(g(1)=1,\;g(2)=1\)なので、$$g(1) = 0.5A_1 + 0.2 A_2 = 1 \\ g(2) = 0.25A_1 + 0.04A_2 = 1$$である。この2式から、\(A_1 = 16/3 , \;\;\; A_2 = -25/3\)が求まる。従って、$$g(k) = \frac{16}{3} \left(\frac{1}{2}\right)^k - \frac{25}{3} \left(\frac{1}{5} \right)^k \;\;\;\; (k \ge 3)$$となる。
Scilabによる解法
clear; clf;
z=%z; e=%e;
Gz = (z+0.3)/(z^2 -0.7*z +0.1);
//インパルス応答
u= [1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ];
y = flts(u,Gz);
scf(0);plot(y,'-o');
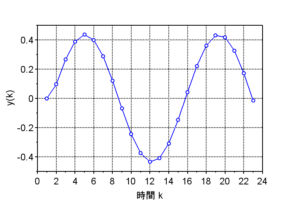
図1に\(G(z)\)のインパルス応答を示す。解法1、2と同じ結果が得られている。ただし、Scilabによる解法では、\(k=1\)で単位インパルスを入力していることに注意。
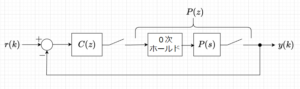
0次ホールドを使用した離散時間制御系の時間応答
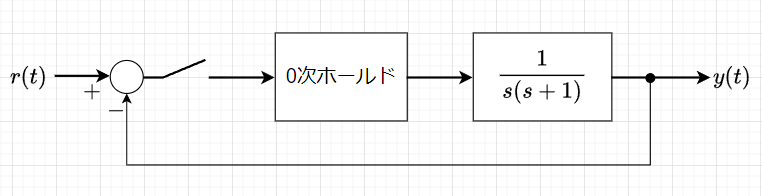
図2で示す制御系のステップ応答を求める。
\(P(s) = \frac{1}{s(s+1)}\)について、0次ホールドを使用した離散化システムの伝達関数\(P(z)\)は、$$P(z) = (1 - z^{-1})\mathcal{Z}\left[\frac{1}{s^2(s+1)}\right] \\=\frac{(T + e^{-T} -1)z+(1 +e^{-T} - Te^{-T})}{(z-1)(z-e^{-T})}$$ となる。また、閉ループ伝達関数\(T(z)\)は、$$T(z) = \frac{P(z)}{1 + P(z)}$$となる。従って、ステップ応答は、$$Y(z) = \frac{z}{z-1} T(z)$$を逆Z変換することで求まる。
Scilabによる計算
以下のスクリプトで、\(T=0.1,\;0.5,\;1.0 \)と変えて、ステップ応答を求める。
-----------------------------------------------------------
clear; clf;
z=%z; e=%e; s=%s;
Ps = 1/(s*(s+1));
Ts = Ps/(1+Ps); /* 閉ループ伝達関数 */
//連続時間系ステップ応答
// 0からETまで0.01刻みでtを設定
ET=20;
t=0:0.01:ET;
y=csim('step',t,Ts); /* 線形シミュレーション */
scf(0);plot(t,y);
T=0.1; /* サンプリング時間*/
N=ET/T; /* サンプリング点数*/
Pz = ((T+e^(-T)-1)*z + (1 - e^(-T)- Te^(-T))) / ((z-1)*(z-e^(-T)));
Tz = Pz/(1+Pz); /* 閉ループ伝達関数 */
//離散時間系ステップ応答
k=1:N; /* サンプリング点*/
r(k)=1; r=r'; /*ステップ入力 */
y = flts(r,Tz); /*離散時間シミュレーション*/
scf(1);plot(y,'-o');
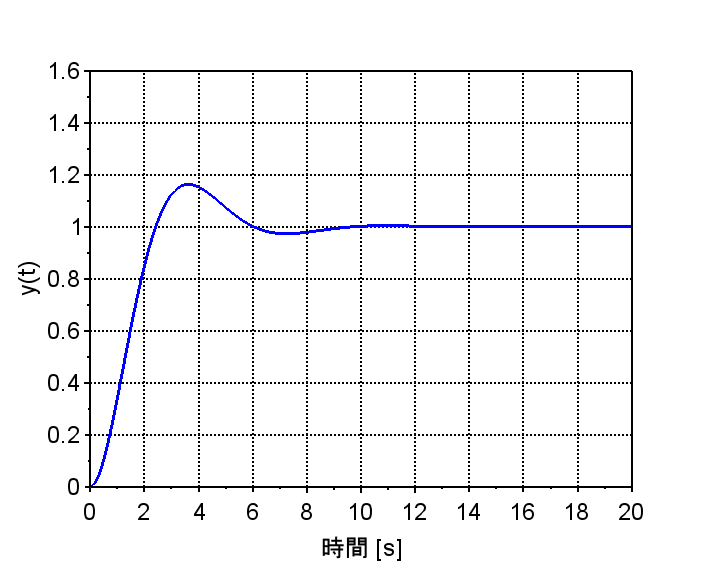
図3は、連続時間系のステップ応答である。2次系なのでオーバーシュートが見られるが、安定に目標値(ステップ入力)に到達している。
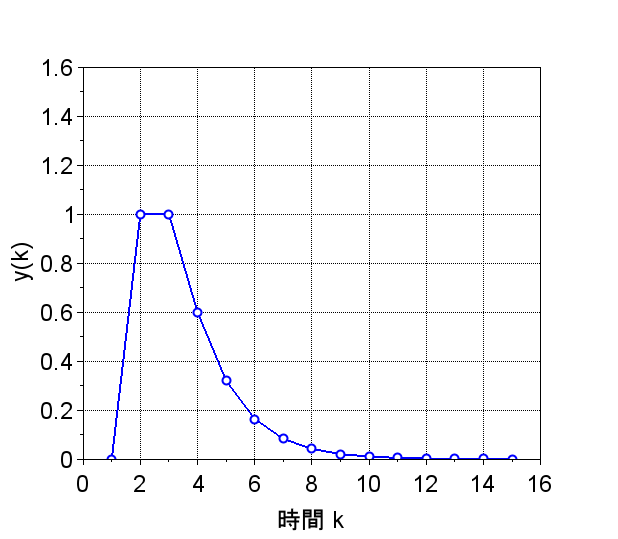
図4は、図2に示す0次ホールドを使用した離散時間系で、サンプリング時間を\(T=0.1 [s]\)に設定した場合のステップ応答である。この場合は、連続時間系とほぼ同等のステップ応答特性を実現できている。図5はサンプリング時間を\(T=0.5 [s]\)に設定した場合のステップ応答である。オーバーシュートがやや大きくなり、応答の劣化が見られるが、目標値には安定に到達している。図6はサンプリング時間を\(T=1.0 [s]\)に設定した場合のステップ応答である。オーバーシュートが大きく、振動も長い時間となり、応答の劣化が見られる。目標値には安定に到達している。なお、サンプリング時間を約\(T=3.0 [s]\)以上にすると不安定となる。
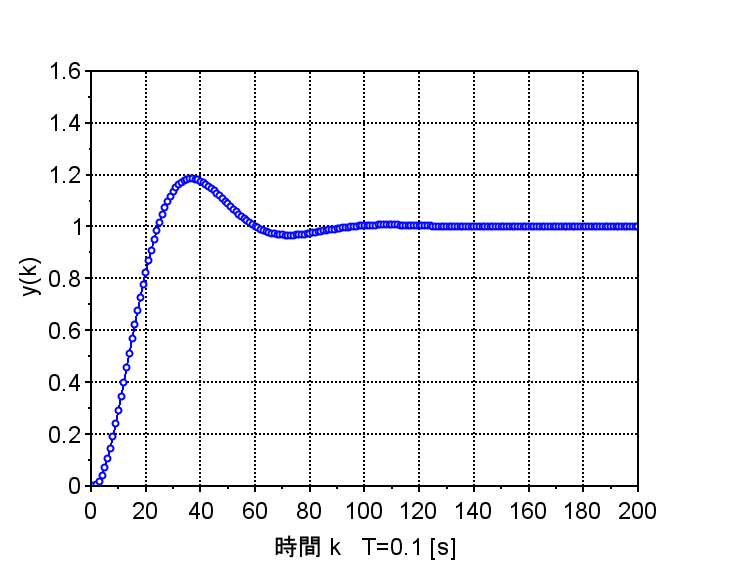
T=0.1 [s]
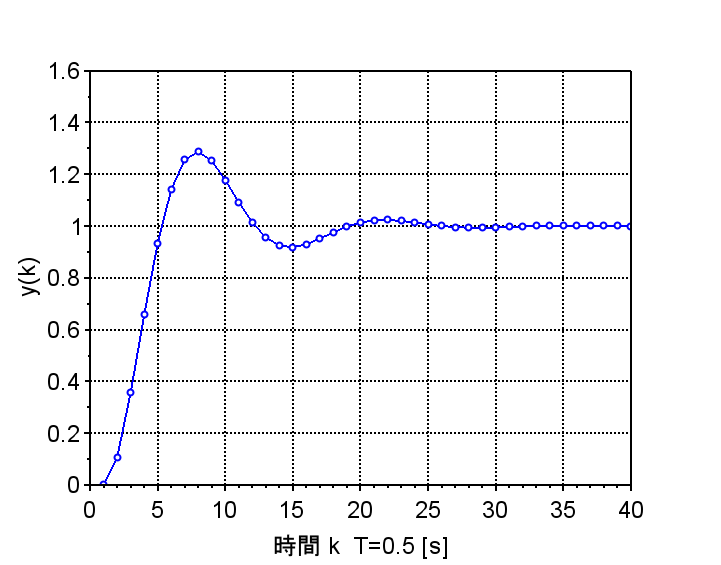
T=0.5 [s]
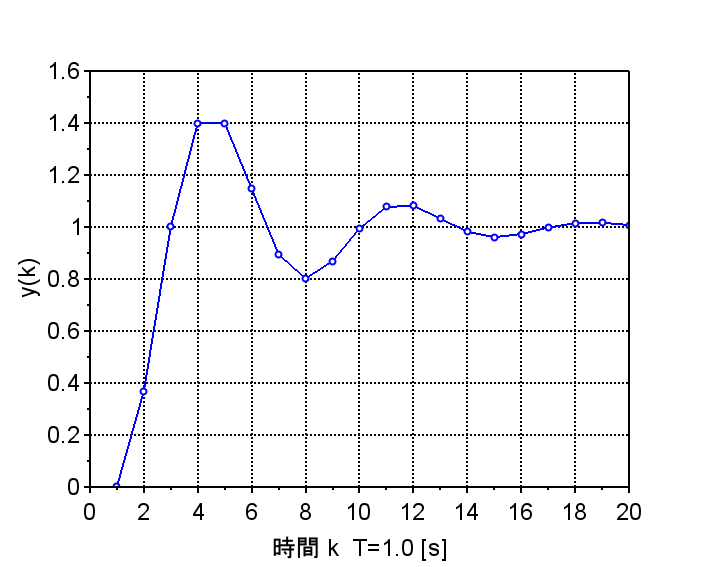
T=1.0 [s]