7-1. 離散時間システムの定常特性（演習）

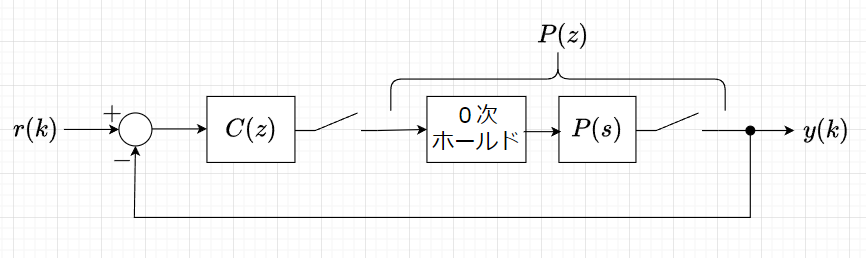
$$P(s) = \frac{1}{s+1}$$の1次系とする。
＊図１において、０次ホールドを使用して離散化した\(P(s)\)を求める。
$$P(z) = (1 - z^{-1})\mathcal{Z} \left\{\frac{1}{s(s+1)} \right\} = (1 - z^{-1})\mathcal{Z} \left\{ \frac{1}{s} - \frac{1}{s+1} \right\} \\ =\frac{z-1}{z} \left(\frac{z}{z-1} - \frac{z}{z - e^{-T}} \right) = \frac{1 - e^{-T}}{z - e^{-T}}$$

＊制御器を\(C(z) =K \frac{z- \mu}{z-1}\)として、閉ループ伝達関数と特性方程式を求める。
$$L(z) = C(z)P(z) = K\frac{z- \mu}{z-1} \cdot \frac{1 - e^{-T}}{z - e^{-T}} = K\frac{(z- \mu)(1 - e^{-T})}{(z-1)(z-e^{-T})}$$閉ループ伝達は、$$T(z) = \frac{L(z)}{1 + L(z)}$$ \(p=e^{-T}\)とおいて、$$T(z) = \frac{K(z-\mu)(1-p)}{z^2 - \left\{K(1-p) -1-p \right\}z + p - K \mu(1-p)}$$となる。従って、特性方程式は、 $$z^2 - \left\{K(1-p) -1-p \right\}z + p - K \mu(1-p) = 0$$である。

＊閉ループ系の極が、\(\lambda_1 = 0, \; \lambda_2 =0\)となる、\(K, \; \mu\)を求める。
極が０（２重極）になるためには、特性方程式より、$$K(1-p)-1-p = 0 , \;\;\;\;\;\; p - K \mu(1-p)=0$$となればよい。よって、$$K = \frac{1+p}{1-p} , \;\;\;\; \mu = \frac{p}{1+p} \;\;\;\;\;\;\;\; (p=e^{-T})$$である。

＊閉ループ伝達関数を求めると。
$$T(z) = \frac{(1+p)z-p}{z^2}$$である。

＊ステップ応答、ランプ応答を求める。
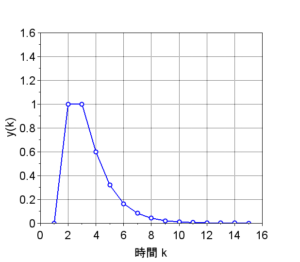
ステップ応答：ステップ入力は、\(R(z) = \frac{z}{z-1}\)なので、ステップ応答\(Y_1(z)\)は、$$Y_1(z) = R(z)T(z) = \frac{(1+p)z - p}{z(z-1)} = (1+p)z^{-1} + \sum_{i=2}^{\infty} z^{-i}$$である。
ランプ応答：ランプ入力は、\(R(z) = \frac{Tz}{(z-1)^2}\)なので、ランプ応答\(Y_2{z}\)は、$$Y_2(z) = R(z)T(z) = T \frac{(1+p)z -p}{z(z-1)^2} = T \sum_{i=1}^{\infty} (i + p)z^{-(i+1)}$$である。

Scilabによる時間応答

\(T=0.1\)（\(p=0.90484\)）とする。
ーーーーーーーーーーーーーーーーーーーーー
clear; clf;
z=%z;e=%e;s=%s;
T=0.1; /*サンプリング時間*/
p=e^(-T);
K=(1+p)/(1-p); m=p/(1+p);
Cz=K*(z-m)/(z-1); /* 制御器 */
Pz=(1-p)/(z-p);
Lz=Cz*Pz; /* 開ループ伝達関数 */
Tz=Lz/(1+Lz); /* 閉ループ伝達関数*/
ET=1; /*シミュレーション時間*/
n=ET/T; /* サンプリング点数*/
//離散時間系ステップ応答
k=1:n; /* サンプリング点*/
r(k)=1; r1=r'; /* ステップ入力 */
y = flts(r1,Tz); /* 離散時間シミュレーション*/
scf(0);plot(y,'-o');
//離散時間系ランプ応答
k=1:n; /* サンプリング点*/
r(k)=k; r2=r'; /*ランプ入力 */
y = flts(r2,Tz); /* 離散時間シミュレーション*/
scf(1);plot(y,'-o');

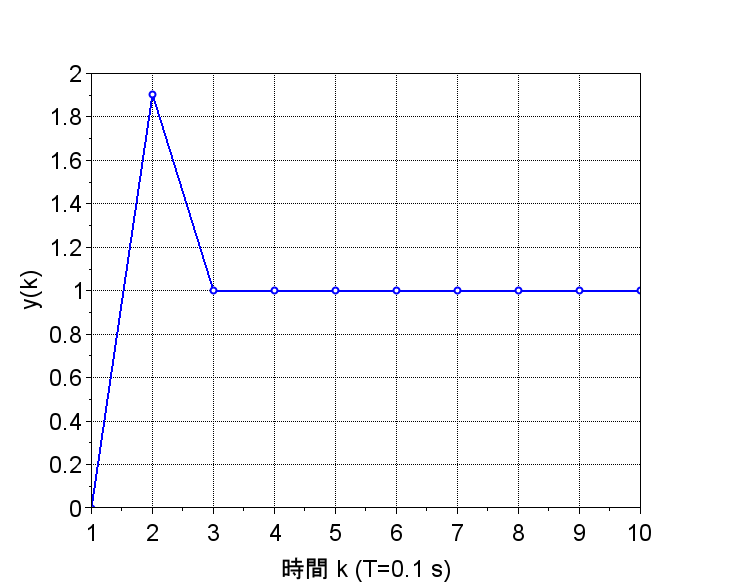
ステップ応答（図２）では、目標値（（\r=1\)）に安定に到達しているが、ランプ応答（図３）では、安定に目標値に向かって動作しているが、定常偏差が残っている。

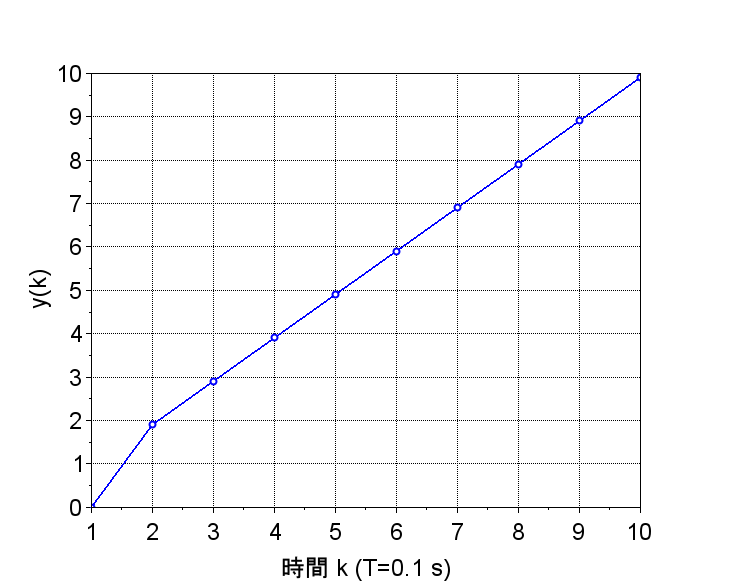
＊定常速度偏差（ランプ入力に対する偏差）を求める。
7. 離散時間システムの定常特性より、定常速度偏差定数は、$$K_v = \frac{1}{T} \lim_{z \rightarrow 1} (z-1)L(z) = \frac{K(1 - \mu)}{T}$$となるので、ランプ入力に対する定常偏差は、$$e_v = \frac{1}{K_v} = 0.09516T$$となる。