14-1. 状態観測器(演習)
可制御、可観測の双対性 可制御性と可観測性の双対性とは、これらの2つの性質が密接な関係を持っていることを意味し、システムの可制御性に関する問題を、対応する「双対」システムにおける可観測性の問題に置き換えて考えることができ […]
12-1. 状態フィードバック制御(演習)
離散時間システムの状態フィードバック制御 離散時間システムが、$$x(k+1) = \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0. […]
9-1. 可制御性、可観測性(演習)
離散時間システムの可制御、可観測条件 連続時間システムの状態方程式が、$$\frac{dx}{dt} = \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix} x + […]
8-1. 離散時間システムの安定性(演習)
離散時間システムの安定性の基準 離散時間システムの特性方程式のすべての根(固有値、伝達関数の極)が単位円の内側に存在する場合、そのシステムは安定である。特性方程式の形は次のように表される。$$\phi(z) = a_0 […]
7-1. 離散時間システムの定常特性(演習)
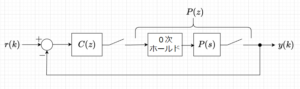
$$P(s) = \frac{1}{s+1}$$の1次系とする。*図1において、0次ホールドを使用して離散化した\(P(s)\)を求める。$$P(z) = (1 - z^{-1})\mathcal{Z} \left\{\ […]
5-1. 離散時間システムの応答(演習)
離散時間システムのインパルス応答 離散時間伝達関数が、$$G(z) = \frac{z + 0.3}{z^2 - 0.7z +0.1}$$のシステムのインパルス応答を求める。 解法1:$$G(z) = \frac{Y(z […]
4-1. 連続時間システムの離散化(演習)
連続時間伝達関数の離散時間伝達関数への変換 (1)\(G(s) = \frac{K}{s}\)を0次ホールドを含む離散化システムに変換する。$$G(z) = (1 - z^{-1})\mathcal{Z}\left\{\ […]
2-1. 留数定理によるZ変換
※以下、虚数単位に「\(j\)」を使用する。 留数定理 留数定理は、特異点の周りで関数を積分する際に、その点における関数の「留数」(Residue:何かが取り除かれた後に残っているもの、という意味)を利用するものである。 […]
1-1. 離散時間制御系の構成(演習)
連続時間システムから離散時間システムへの変換 連続時間システムが微分方程式$$\frac{dy}{dt} = \alpha y + \beta u \;\; \cdots (1)$$で与えられるとき、このシステムをディジ […]
2. 行列式(線形代数)
行列式とは、正方行列に対して定義される量で、歴史的には行列が表す一次方程式の可解性を判定する指標として導入された。幾何的には、線型変換に対して線形空間の拡大率ということができる。つまり、行列式は、行列がどれくらい空間を「 […]
1. 行列と行列の演算(線形代数)
線形代数は、ベクトル空間と線形写像に関する理論と応用を扱う。制御工学、特に現代制御理論では重要な数学ツールとなっている。線形代数は、次の概念や操作を含む。1.ベクトルとベクトル空間:ベクトルは数値の集合であり、方向と大き […]
24. 極配置法(演習)
式(1)で表記する1入力\(n\)次元定係数線形システムを制御対象とする。$$\dot{x}(t) = A x(t) + b u(t) \\ y(t) = c x(t) \;\;\cdots \cdots (1)$$式( […]
23. 可観測性(演習)
※可観測性の解説は、11. 可観測性 、9. 対角正準形 を参照願います。 システムを$$\dot{x}(t) = A x(t) + b u(t) \\ y(t) = cx(t) \;\; \cdots \cdots ( […]
22. 可制御性(演習)
※可制御性の解説は、10. 可制御性、12. 可制御正準系 を参照願います。※固有値、固有ベクトルの計算手順の詳細については、固有値と固有ベクトルの計算 を参照願います。 座標変換 1入力1出力\(n\)次元システム $ […]
21. システムの応答(演習)
制御対象を入力\(m\)、出力\(l\)の\(n\)次元の線形定係数システムとする。$$\dot{x}(t) = A x(t) + B u(t) \;\cdots \cdots (1) \\ y(t) = C x(t)\ […]
20. システムの状態方程式(演習)
システムの特性を以下の状態方程式(式(1))、出力方程式(式(2))で表現する。$$\dot{x}(t) = A x(t) + B u(t) \;\;\cdots \cdots (1)\\y(t) = C x(t) \; […]
※ラプラス変換、Z変換表
連続時間信号\(x(t)\)に対するラプラス変換、離散時間信号に対する\(Z\)変換の表を示す。離散時間信号は、\(x(t)\)をサンプリング周期\(T\)でサンプリングした信号とする。また、以下の表で\(a=e^{-\ […]
6-1. 畳み込み積分のラプラス変換
畳み込み積分(Convolution Integral)は、制御工学、信号処理、画像処理などの分野でよく使われる数学的な操作である。畳み込みは、2つの関数を組み合わせて新しい関数を生成する操作となっている。2つの連続関数 […]
38-1. I-P制御
PI制御(Integral-Proportional Control)(I-P制御はPI制御と異なる部分もあるが、制御要素は共通である)は、比例制御(P制御)と積分制御(I制御)の2つの要素を組み合わせた制御方法で、制御 […]
19. 最適フィードバック制御
最適フィードバック制御は、制御系の性能を評価する関数(評価関数)を設定し、その関数値を最小化するようにフィードバックゲインを決定する制御方法である。評価関数は、制御系の応答の振る舞いを反映した関数で、応答の速度、精度、安 […]