17. 離散時間系の最適レギュレータ
最適レギュレータは、制御理論において、システムの状態を効率的に制御するためのフィードバック制御法である。システムの性能指標(評価関数)を最小化しつつ、システムの安定性や性能を最適化することを目的とする。 最適レギュレータ […]
14-1. 状態観測器(演習)
可制御、可観測の双対性 可制御性と可観測性の双対性とは、これらの2つの性質が密接な関係を持っていることを意味し、システムの可制御性に関する問題を、対応する「双対」システムにおける可観測性の問題に置き換えて考えることができ […]
12-1. 状態フィードバック制御(演習)
離散時間システムの状態フィードバック制御 離散時間システムが、$$x(k+1) = \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0. […]
9-1. 可制御性、可観測性(演習)
離散時間システムの可制御、可観測条件 連続時間システムの状態方程式が、$$\frac{dx}{dt} = \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix} x + […]
8-1. 離散時間システムの安定性(演習)
離散時間システムの安定性の基準 離散時間システムの特性方程式のすべての根(固有値、伝達関数の極)が単位円の内側に存在する場合、そのシステムは安定である。特性方程式の形は次のように表される。$$\phi(z) = a_0 […]
7-1. 離散時間システムの定常特性(演習)
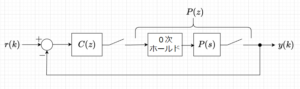
$$P(s) = \frac{1}{s+1}$$の1次系とする。*図1において、0次ホールドを使用して離散化した\(P(s)\)を求める。$$P(z) = (1 - z^{-1})\mathcal{Z} \left\{\ […]
5-1. 離散時間システムの応答(演習)
離散時間システムのインパルス応答 離散時間伝達関数が、$$G(z) = \frac{z + 0.3}{z^2 - 0.7z +0.1}$$のシステムのインパルス応答を求める。 解法1:$$G(z) = \frac{Y(z […]
4-1. 連続時間システムの離散化(演習)
連続時間伝達関数の離散時間伝達関数への変換 (1)\(G(s) = \frac{K}{s}\)を0次ホールドを含む離散化システムに変換する。$$G(z) = (1 - z^{-1})\mathcal{Z}\left\{\ […]
2-1. 留数定理によるZ変換
※以下、虚数単位に「\(j\)」を使用する。 留数定理 留数定理は、特異点の周りで関数を積分する際に、その点における関数の「留数」(Residue:何かが取り除かれた後に残っているもの、という意味)を利用するものである。 […]
1-1. 離散時間制御系の構成(演習)
連続時間システムから離散時間システムへの変換 連続時間システムが微分方程式$$\frac{dy}{dt} = \alpha y + \beta u \;\; \cdots (1)$$で与えられるとき、このシステムをディジ […]
※ラプラス変換、Z変換表
連続時間信号\(x(t)\)に対するラプラス変換、離散時間信号に対する\(Z\)変換の表を示す。離散時間信号は、\(x(t)\)をサンプリング周期\(T\)でサンプリングした信号とする。また、以下の表で\(a=e^{-\ […]
16. ディジタル再設計
制御器の設計におけるディジタル再設計とは、アナログ制御の方法をディジタル技術を利用した制御に変更することを指す。従来のアナログ制御では、制御信号は電圧や電流の変化で表現されていたが、ディジタル制御では信号をディジタルデー […]
15. 状態観測器に基づいた制御系
状態観測器に基づいた制御系は、制御対象の状態量を観測することで、操作量を生成する制御システムである。この制御系では、状態フィードバック制御を基本として、制御対象の状態変数をフィードバックすることで、制御対象の安定化と望ま […]
13. デッドビート制御
デッドビート制御とは有限時間整定制御とも呼ばれ、出力と目標値の偏差を有限ステップ内で零に整定させるディジタル制御手法である。デッドビート制御では、応答が目標値に到達するまでの過渡現象を完全に抑制させることを目指し、定常状 […]
12. 状態フィードバック制御
離散時間系の状態フィードバックは、システムの状態変数を測定し、その情報を使用してシステムを制御する方法である。この方法は、システムの安定化や望ましい挙動(適切な極配置)を達成するために使用される。状態フィードバック制御で […]
11. 可制御正準形と可観測正準形
可制御正準形 可制御正準形とは、状態空間表現を用いたシステムのうち、制御入力によって任意の状態に達することができる最も単純な形式の一つである。可制御正準形では、制御入力がシステムの全ての状態変数に対して影響を与えることが […]
10. システムの正準形と等価変換
等価変換 離散時間システムの状態方程式、出力方程式を$$x(k+1)=Ax(k) + bu(k) \\ y(k)=cx(k) \;\;\;\; \;\;\;\;\; \cdots \cdots (1)$$とする。ある正則 […]
9. 離散時間システムの構造
システムの構造で重要な、可到達性、可制御性、可観測性について説明する。 可到達性、可制御性 離散時間システム\(x(k+1)=Ax(k)+bu(k)\) において、原点\(x(0)=0\)から、時刻\(n\)において任意 […]
8. 離散時間システムの安定性
インパルス応答が時間の経過とともに零に収束すれば、線形システムは安定である。離散時間システムのパルス伝達関数は、$$G(z) = \frac{b_0 z^m + b_1 z^{m-1} + \cdots + b_m}{z […]